$\Huge\color{orchid}{点击此处获取更多干货}$

DAG游戏与SG数

虽然本问题的背景仍然是若干堆石子以及先拿完者获胜，但拿的石子数量不再任意，而是被限定在了某些数量上，那么相比于一般的nim游戏，每一种局面可转移到的下一种局面数量就变得更加有限了，此时的游戏更像是一种有向图（DAG）游戏，每一种局面就是该图的一个节点，局面之间的转移就是图的边，出现无法继续转移的状态时，当前轮到的玩家失败。

将每一堆石子分立的来看，如果每次可取走的石子数量为$\{2,3\}$，那么石堆大小为2或3时，对于先手玩家是等价的，因为只需要进行一次操作，留给后手玩家的就是0或1这种失败状态，此时2和3可以视作1级胜利状态；而石堆大小为4时，先手可以取走2变为1级胜利状态2，也可以取走3变为失败状态1，那么4就相当于2级胜利状态。本帖中，就用“$X$级胜利”代替$N$和$P$来表示状态。其中$X=0$时对应的是失败状态，而一个状态为$X$级的充要条件是它可以转化到$0\sim X-1$的任意一级。

定义完每一堆石子上的“X级胜利状态”后，再考虑一下两堆石子的组合，重点关注对象是状态的级数$X$。易知两个0对应的还是0（失败），而1和0的组合为1（胜利），因为先手只需通过一步操作将局面变为两个0的组合，就能获得胜利；两个1的组合又为0（失败），无论先手将哪一个1变为0，后手只要把另一个也变为0，留给先手的依然是0。这样的计算方式，和“异或”运算完全一致，而对于任意级的胜利状态，经过若干次操作后总能变为1，0级。任意堆石子的组合可以沿用该规律，每一堆石子对应级数的异或和为0，则先手必败，反之先手必胜，这和一般nim游戏的规律相似。

最后的问题就是，每一种状态的“级数”如何计算？可以转移到$0\sim X-1$级的状态必然是$X$级，这与之前的定义相同。那么如果某一个状态可以转化到$2\sim X-2$级以及0级，但是不能转化到1级时，根据上面的定义也可以做出判断：满足$0\sim X-1$任意一级的状态都可以由当前状态转移而来的最小$X$，即为该状态的级数，因此该状态为1级。

实际上，上面定义的这个级数，就是$\text{Sprague-Grundy}$数即$\text{SG}$数，任意一个状态$q_x$的$\text{SG}$数计算方法为$SG(q_x)=mex\{SG(q)|q_x\rightarrow q\}$，$mex$表示自然数集合中没有出现的最小自然数。该计算方式涉及递归，考虑到不同状态在计算过程中可能使用到相同的$SG$数，可以把每一个状态的$SG$数记录下来，这种方式在动态规划部分还会进一步介绍。

另外，其实一般的nim游戏也可以转化为本问题中的DAG游戏，虽然没有明确限制取石子的数量，但它包含一个硬性的限制那就是“不能超过石堆大小”，因此一般nim游戏中每一种状态的转移方式也是有限的。用一般nim游戏的规则来计算一下任意状态$q$的$SG$数，那么可以用下图来表示：

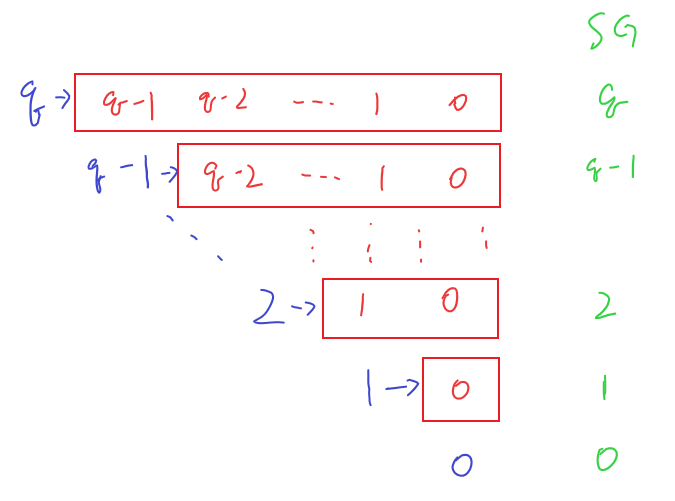
每一个状态的后继SG值都是连续出现的，因此一般nim游戏中$SG(q)=q$，异或和的结论也可以用SG值的异或和来解释。

C++ 代码

#include <iostream>
#include <unordered_map>
#include <unordered_set>
#include <functional>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int k;
    cin >> k;
    int* choice = new int[k];
    for (int i = 0; i < k; i++) cin >> choice[i];
    unordered_map<int, int> memo;               //状态数量在此处还未知，因此使用哈希表
                                                //若状态数量已知，或含有多个维度难以哈希，可以使用初始全-1的定长数组

    function<int(int)> sg = [&](int x)->int {   //递归求sg数
        if (memo.find(x) != memo.end()) {
            return memo[x];                     //已经计算过了的可以直接返回
        }
        unordered_set<int> s;                   //后继状态集合
        for (int i = 0; i < k; i++) {
            if (x >= choice[i]) {               //拿取的数量不能超过石堆大小
                int q = x - choice[i];
                s.insert(sg(q));                //计算并存储后继状态的sg值
            }
        }
        int i = 0;
        while (true) {
            if (s.find(i) == s.end()) {         //找到了不属于该集合的最小自然数
                memo[x] = i;                    //记录在表中，供之后直接取得
                break;
            }
            else i++;
        }
        return memo[x];
    };
    int n, ans = 0;
    cin >> n;
    while (n--) {
        int x;
        cin >> x;
        ans ^= sg(x);
    }
    cout << ((ans != 0) ? "Yes" : "No") << endl;
    return 0;
}