AcWing 120. 防线

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 120. 防线原题链接中等

作者：

墨染空 , 2019-06-22 00:25:45 , 所有人可见 , 阅读 4637

50

9

PS：萌新第一次题解，瑟瑟发抖

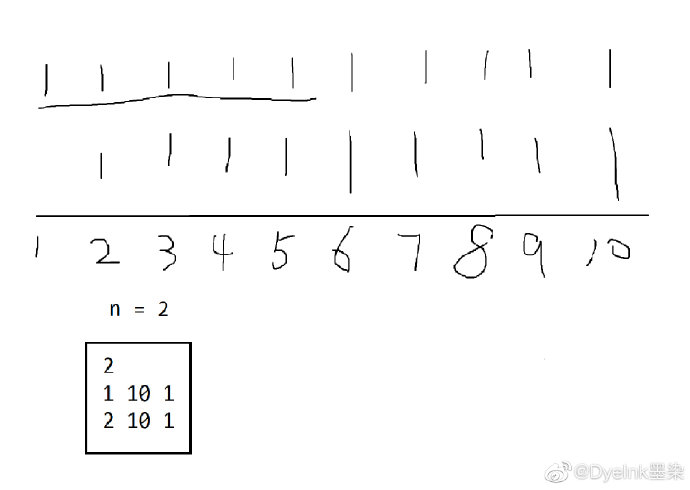
题目简译：给定 $n$ 个等差数列，每个等差数列的起点为 $s$ ，终点为 $e$ ，差为 $d$ 。整个序列中至多有一个位置所占数字是奇数。判断奇数位是否存在，如果不存在输出"There's no weakness."，如果存在输出位置与大小。

温馨提示： $⌊x⌋$ 为将 $x$ 向下取整

算法：前缀和 + 二分位置

1、奇数位存在性

整个序列中至多有一个位置的数字所占数量是奇数，所以如果存在奇数位，则整个数列的总和必然是奇数（奇数 + 偶数 = 奇数，偶数 + 偶数 = 偶数）。反之，若不存在奇数位，则一定是偶数。故只需判断数字数量的总和的奇偶性即可。

2、二分位置

若存在这个奇偶性，我们可以通过二分答案的位置来找到这个位置，然后判断区间 $[l,mid]$ 的总和的奇偶性。若为奇数，则奇数位存在于此区间。反之若为偶数，则一定存在于 $[mid+1,r]$ 区间。用这个方法逐步缩小范围即可。

关于查找 $[l,mid]$ 的总和，我们可以用前缀和的思路，用 $sum[mid] - sum[l-1]$ 即可求出。( $sum[i]$ 为求出 $i$ 位置之前所有位置的和)

3、 $O(n)$ 时间求出区间 $sum[x]$ 的数字个数

设整个数列的最小位置为 $minn$

这里，我们枚举每一个等差数列（它的起点为 $s$ ，终点为 $e$ ，差为 $d$ ）。若 $s <= x$ ，则两区间存在交集。

则它与 $[minn,x]$ 的共同区间为 $[s,min(e,x)]$ 。那么此区间包含此数列的个数是 $⌊(min(e,x) - s) / d⌋ + 1$ 。

正确性证明十分容易：
在此区间中存在一段区间，共 $⌊s,min(e,x) / d⌋ * d$ 个位置，头尾的位置上都有数字，差为 $d$ ，则数字的数量就是 $⌊(min(e,x) - s) / d⌋ + 1$ 。

时间复杂度： $O(nlogn)$

二分的时间为 $O(logn)$ ，每次 $check()$ 的时间为 $O(n)$ ，故总的时间复杂度为 $O(nlogn)$ 。

C++ 代码

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int N = 200000 + 1, INF = 1e9;
int t,n;
struct node{
    int s,e,d;
}a[N];
int getSum(int x){ // O(n) 求[minn,x]的前缀和 
    int res = 0;
    for(int i = 1; i <= n; i++)
        if(a[i].s <= x)
            res += (min(a[i].e, x) - a[i].s)/a[i].d + 1;

    return res;
}
bool check(int l,int r){ // O(n) 查找[l,r]是否存在奇数位 
    return (getSum(r) - getSum(l - 1)) & 1;
}
int main(){
    cin >> t;
    while(t--){
        cin >> n;
        int maxn = -INF, minn = INF;
        for(int i = 1; i <= n; i++){
            cin >> a[i].s >> a[i].e >> a[i].d;
            minn = min(minn,a[i].s); 
            maxn = max(maxn,a[i].e);
        }

        if(!(getSum(maxn) & 1)){
            cout << "There's no weakness." << endl;
        }else{
            int l = minn, r = maxn;
            while(l <= r){
                int mid = (l + r) >> 1;
                if(check(l,mid))r = mid - 1;
                else l = mid + 1;
            }

            cout << l << " " << (getSum(l) - getSum(l - 1)) << endl;
        }
    }
    return 0;
}

24 评论

种花家的纽约市长 2023-01-05 19:35

考古成功！

马丁 2020-10-11 23:43

前两个性质我都想到了，我想的是对于任意的一个区间使用差分来一遍，将所有区间读完，然后求一个前缀和，然后二分答案，结果正准备写代码的时候，发现s和e的范围太大，就无从下手了，哎！

hya 2022-12-02 15:33

世另我,还是思维惯性想着所有区间的前缀和都要求,一看数据范围,铁超时啊,顿时写不下代码了.结果只需要用到哪部分就求那部分.唉

TUTU_ 2024-02-05 16:33

差分也不对吧，比如1 2 5，2 2 6，1 1 6这种情况

秦淮岸灯火阑珊 2019-11-08 20:49

%%%

墨染空 2019-11-08 20:49

哈

秦淮岸灯火阑珊 2019-11-08 20:50 回复了墨染空的评论

# %%%sky大佬高质量题解

墨染空 2019-11-08 20:59 回复了秦淮岸灯火阑珊的评论

(/ω＼)然而现在题解越写越简陋

秦淮岸灯火阑珊 2019-11-08 21:26 回复了墨染空的评论

明明是我好伐

CS萌新 23天前 ·江苏

写得太妙了
我自己做的时候做不出来，看了这个题解。看到用防具个数是否为奇数来二分就没看了，想自己看看能不能想出来，后面虽然做出来了，但是异常复杂。
个人认为这个问题一共有两个困难的点
1.能否想到用奇数偶数来二分（想不到就做不出来）
2.能否想到check函数是用前缀和的思想用total_num(min,r)-total_num(min,l-1)的方法求出(l,r)之间的防具个数。这里这个前缀和真的太巧妙了，平时我们写前缀和仅仅是为了降低时间复杂度，但这里用了前缀和的思想，却没有使用所谓的数组来存放前缀和，只是使用了num[l,r]=num[min,r]-num[min,l-1]这种表达式，真的太巧妙了。我自己的代码写起来麻烦的要死，就是因为没有用前缀和。
以下是我的史山代码：
#include[HTML_REMOVED]
using namespace std;
typedef pair[HTML_REMOVED] PII;
struct caozuo
{
long long s;
long long e;
long long d;
};
//返回1表示这个区间内有漏洞
bool check(vector[HTML_REMOVED] &lst,long long l,long long r)
{
//以下是测试部分
//cout<<”\n现在在判断”<[HTML_REMOVED]r||i.e[HTML_REMOVED]i.s)
{
left=(l-i.s)/i.d;
//刚好有个点位于i.s的位置
if((l-i.s)%i.d==0) total;
right=(r-i.s)/i.d;
total+=right-left;
}
else if(l==i.s)
{
total+=1;
right=(r-i.s)/i.d;
total+=right;
}
else
{
//l[HTML_REMOVED] ans;
int T;
cin>>T;
while(T–)
{
vector[HTML_REMOVED] lst;
int n;
cin>>n;
long long l=0,r=0;
//将n组防具存下来
for(int i=1;i<=n;i)
{
long long a,b,c;
cin>>a>>b>>c;
lst.push_back({a,b,c});
r=max(r,b);
}
while(l[HTML_REMOVED]l) continue;
//说明该位置上面有防具
if ((l-i.s)%i.d==0 && l<=i.e) total+=1;
}
if(total%2==1)
{
ans.push_back({l,total});
}
else
{
ans.push_back({-1,-1});
}
}
for(auto i:ans)
{
if(i.first==-1)
{
cout<<”There’s no weakness.”<<endl;
}
else
{
cout<<i.first<<” “<<i.second<<endl;
}
}
return 0;
}

化倾 2023-07-16 21:37

贴个py

from typing import *
from math import *
def I():
    return input()

def II():
    return int(input())

def MII():
    return map(int, input().split())

def LI():
    return list(input().split())

def LII():
    return list(map(int, input().split()))

def GMI():
    return map(lambda x: int(x) - 1, input().split())

def LGMI():
    return list(map(lambda x: int(x) - 1, input().split()))
# start-----------------------------------------------------
# 二分法
# 首先统计出防具总数量sum，当sum为偶数时必不存在唯一一个破绽点，只要当sum为奇数时存在
# 二分范围为[min(s),max(e)] 即[l,r]，当[l,mid]的范围内防具总数psum为奇数则r = mid
def slove():
    n = II()
    g = []
    sum = 0
    l,r = inf,-inf
    for _ in range(n):
        s,e,d = MII()
        g.append((s,e,d))
        l,r = min(s,l),max(e,r)
        sum += (e-s)//d + 1
    if sum & 1 == 0:
        print("There's no weakness.")
        return
    while l < r:
        mid = (l + r) >> 1
        psum = 0
        for s,e,d in g:
            if mid >= e:
                psum += (e-s)//d + 1
            elif mid >= s and mid < e:
                psum += (mid-s)//d + 1
        if psum & 1:
            r = mid
        else:
            l = mid + 1
    p,c = l,0
    for s,e,d in g:
        if p >= s and p <= e and (p-s) % d == 0:
            c += 1
    print(p,c)


T = II()
while T:
    T-= 1
    slove()
# end-------------------------------------------------------