题目描述

现有一个有序数组，假设从某个数开始将它后面的数按顺序放到了数组前面。
(即 [0,1,2,4,5,6,7] 可能变成 [4,5,6,7,0,1,2])。

请找出数组中的最小元素。

数组中可能包含重复元素。

样例1

输入：[1,3,5]
输出：1

样例2

输入：[2,2,2,0,1]
输出：0

算法

(二分) $O(n)$

类似于Find Minimum in Rotated Sorted Array，为了避免处理边界情况，我们在数组长度小于5时直接线性扫描出最小值。

为了便于分析，我们先将数组中的数画在二维坐标系中，横坐标表示数组下标，纵坐标表示数值，如下所示：

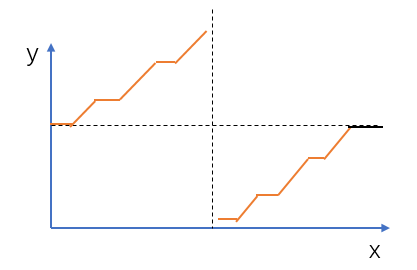
图中水平的实线段表示相同元素。

我们发现除了最后水平的一段（黑色水平那段）之外，其余部分满足二分性质：竖直虚线左边的数满足 $nums[i] \ge nums[0]$ 并且 $nums[i] \gt nums[n-1]$，其中 $nums[n-1]$ 是数组最后一个元素；而竖直虚线右边的数不满足这个条件。分界点就是整个数组的最小值。

所以我们先将最后水平的一段删除即可。

另外，不要忘记处理数组完全单调的特殊情况。

时间复杂度分析：二分的时间复杂度是 $O(logn)$，删除最后水平一段的时间复杂度最坏是 $O(n)$，所以总时间复杂度是 $O(n)$。

C++ 代码

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while (l < r && nums[r] == nums[l]) r -- ;
        // 其实这块写r - l + 1 < 2就OK，不过思考的时候可以偷个懒，直接把小于5的全部特盘掉了。
        if (r - l + 1 < 5)
        {
            int res = INT_MAX;
            for (int x : nums) res = min(res, x);
            return res;
        }
        if (nums[0] <= nums[r]) return nums[0];
        else
        {
            int end = nums[r];
            while (l < r)
            {
                int mid = (l + r + 1) / 2;
                if (nums[mid] >= nums[0]) l = mid;
                else r = mid - 1;
            }
            return nums[r + 1];
        }
    }
};