$$【组合数学】专题笔记目录$$

这是我做过最难的一题了，真的是推的天昏地暗。

题目大意

现在给你 $n$ 个盒子，每个盒子里放着 $a_i$ 个物品，总货物数量 $S=\sum_{i=1}^n a_i$。
你想通过一系列操作让每个盒子里变成 $b_i$ 个物品，满足 $\sum_{i=1}^n b_i = S$。
每次操作可以把一个盒子中的一个物品移动到它相邻的盒子中，对 $i,i+1$ 号两个盒子做一次操作的代价是 $w_i$。
显然盒子中的物品数量在任意时刻都不能为负数。

你需要对每一种 $b$ 求出操作代价最小值的和。若设 $val(b_1,b_2,\dots,b_n)$ 为让第 $i$ 个盒子刚好有 $b_i$ 个物品的最小代价，那么你需要求出所有满足 $\sum_{i=1}^n b_i = S$ 的非负整数数组 $b$ 的 $\sum \limits _{b} val(b_1,b_2,\dots,b_n)$。

题解

假设已知 $a,b$。考虑现在已经让前 $i-1$ 个盒子满足条件，然后需要在 $i$ 和 $i+1$ 之前移动，则显然：$ans=\sum\limits_{i=1} ^{n-1} w_i \Bigg| \sum\limits_{j=1}^i a_j - \sum\limits_{j=1}^i b_j \Bigg|$

考虑先消掉一层循环，观察到 $\sum\limits_{j=1}^i a / b_j$ 都是一个数组的前缀和形式，所以设 $c,d$ 分别为 $a,b$ 的前缀和，在已知 $a,b$ 的情况下答案可以转化为：$ans=\sum\limits_{i=1} ^{n-1} w_i | c_i - d_i |$
由于 $b$ 未知，因此 $d$ 也是未知的，那么答案就是 $\sum\limits_{d} \sum\limits_{i=1}^{n-1} w_i | c_i - d_i |$

观察第二层循环，我们枚举了 $i$，而由于 $a_i$ 已知，所以 $c_i$ 也是已知。所以考虑枚举 $d_i$ 的方案数，这里令 $cnt(i, d_i)$ 为方案数，则把外层循环扔到里面，答案可以表示为 $\sum\limits_{i=1}^{n-1} w_i \sum\limits_{d_i=0}^S | c_i - d_i | \times cnt(i, d_i)$。
考虑从 $d$ 数列的性质进行分析，会发现由于 $b$ 是非负整数组，$0 \leq d_1 \leq d_2 \leq \dots \leq d_i \dots \leq d_n = S$。
由于我们枚举 $d_i$，并且 $d_n=S$ 是已知，所以数列可以分为 $[1,i)$ 和 $(i,n)$。

接下来考虑求出 $0 \leq d_1 \leq d_2 \leq \dots \leq d_i$ 解的数量。
于是你会发现这个 $\leq$ 让你非常难受。怎么办呢？转化一下 【组合数学】8 种盒中放球问题详解，这相当于是第四条，把若干个相同的物品放入几个不同的盒子，盒子允许为空的问题。
这一步转化很重要，我们以 $i$ 为分界点，左边 $[1,i)$ 有 $(i-1)$ 个数的方案数就是 $\binom{d_i + i - 1}{i - 1}$，右边 $(i,n)$ 有 $n - i - 1$ 个数的方案数就是 $\binom{S + n - d_i - i - 1}{n - i - 1}$。

有了这两个式子，再代入 $cnt(i,d_i)$ 就可以得出答案：

$$ans=\sum\limits_{i=1}^{n-1} w_i \Bigg( \sum\limits_{d_i=0}^S | c_i - d_i | \times \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1} \Bigg)$$

由于 $|x-y| = 2 \times (x-y) + (y-x)$（至于证明，自己手推一下 $x-y$ 的正负性），所以：

$$ans=\sum\limits_{i=1}^{n-1} w_i \Bigg( 2 \times \sum\limits_{d_i=0}^{c_i} (c_i - d_i) \times \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1} + \sum\limits_{d_i=0}^S (d_i - c_i) \times \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1}\Bigg)$$

这个式子过于复杂，我们设：

$$f(n,S,i,k)=\sum\limits_{d_{i}=0}^k \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1}$$
$$g(n,S,i,k)=\sum\limits_{d_{i}=0}^k d_i \times \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1}$$

代回答案，则化简为：

$$ans=\sum\limits_{i=1}^{n-1} w_i \Bigg( 2 \times c_i \times f(n,S,i,c_i) - 2 \times g(n,S,i,c_i) + g(n,S,i,S) - c_i \times f(n,S,i,S) \Bigg)$$

但是这仍然不是很好求，所以我们考虑求出 $f,g$ 两个函数的关系。

$$g(n,S,i,k)=\sum\limits_{d_{i}=0}^k d_i \times \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1}$$
由于 $d_0 = 0$ 所以忽略这一位的贡献；另外有 $C_n^m = C_n^{n-m}$，由此转化式子：
$$=\sum\limits_{d_{i}=1}^k d_i \times \binom{d_i + i - 1}{d_i} \times \binom{S + n - d_i - i - 1}{n - i - 1}$$
把 $d_i$ 和第一个组合数拆成阶乘的式子：$d_i \times \frac{(d_i + i - 1)!}{d_i ! (i - 1) !}$。
上下同时乘 $i$：$d_i \times \frac{(d_i + i - 1)! \times i}{d_i ! i !}$。
化简：$i \times \frac{(d_i + i - 1)!}{(d_i-1)! (i-1)!} = i \times \binom{d_i + i - 1}{i}$。

代入原式：

$$g(n,S,i,k)=\sum\limits_{d_{i}=1}^k i \times \binom{d_i + i - 1}{i} \times \binom{S + n - d_i - i - 1}{n - i - 1}$$

我们当然是要求 $g,f$ 两个函数的关系，所以要把 $g$ 转化为 $f$ 的形式。
观察到 $\binom{d_i + i - 1}{i}$ 中下面的 “$i$” 并不与上面 “$i - 1$” 相等，所以考虑把所有的 $d_i$ 都 $-1$。
同时把公因式 $i$ 提出来。
于是可得：

$$g(n,S,i,k)=i \times \sum\limits_{d_{i}=0}^{k-1} \binom{d_i + i}{i} \times \binom{S + n - d_i - i - 2}{n - i - 1}$$

可以转化为 $f$ 的形式：

$$g(n,S,i,k)=i \times f(n + 1, S - 1, i + 1, k - 1)$$

这样我们就只要维护 $f$ 函数就行了。先把答案抄过来：

$$ans=\sum\limits_{i=1}^{n-1} w_i \Bigg( 2 \times c_i \times f(n,S,i,c_i) - 2 \times g(n,S,i,c_i) + g(n,S,i,S) - c_i \times f(n,S,i,S) \Bigg)$$
$$=\sum\limits_{i=1}^{n-1} w_i \Bigg( 2 \times c_i \times f(n,S,i,c_i) - 2 \times i \times f(n+1,S-1,i+1,c_i-1) + i \times f(n+1,S-1,i+1,S-1) - c_i \times f(n,S,i,S) \Bigg)$$
$$=\sum\limits_{i=1}^{n-1} w_i \Bigg( c_i \times \Big( 2 \times f(n,S,i,c_i) - f(n,S,i,S) \Big) + i \times \Big( f(n+1,S-1,i+1,S-1) -2 \times f(n+1,S-1,i+1,c_i-1) \Big) \Bigg)$$

这个式子看起来就非常的不可做，但是可以发现当中的 $i$ 和 $c_i$ 都是单调不降的。
所以考虑增量维护这些 $f$。

显然四个参数中，前两个是定值，所以只需要考虑后两个的变化。现在想如何通过 $f(n,S,i,k)$ 推导出 $f(n,S,i,k+1)$ 和 $f(n,S,i+1,k)$。

非常显然地，根据定义可以求出 $f(n,S,i,k+1)=f(n,S,i,k) + \binom{(k+1)+i-1}{i-1} \times \binom{S-(k+1)+n-i-1}{n-i-1}$。即：

$$f(n,S,i,k+1)=f(n,S,i,k) + \binom{k+i}{i-1} \times \binom{S-k+n-i-2}{n-i-1}$$

而对于通过 $f(n,S,i,k)$ 推导 $f(n,S,i+1,k)$，我们探究它的组合意义。
由于前面定义 $f(n,S,i,k)=\sum\limits_{d_{i}=0}^k \binom{d_i + i - 1}{i - 1} \times \binom{S + n - d_i - i - 1}{n - i - 1}$，会发现 $f(n,S,i,k)$ 即在坐标轴上只能向右或向上走，从 $(0,0) \rightarrow (i-1,d_i) \rightarrow (i,d_i) \rightarrow (n-1,S)$ 的方案数。

画出示意图（奇丑无比）：

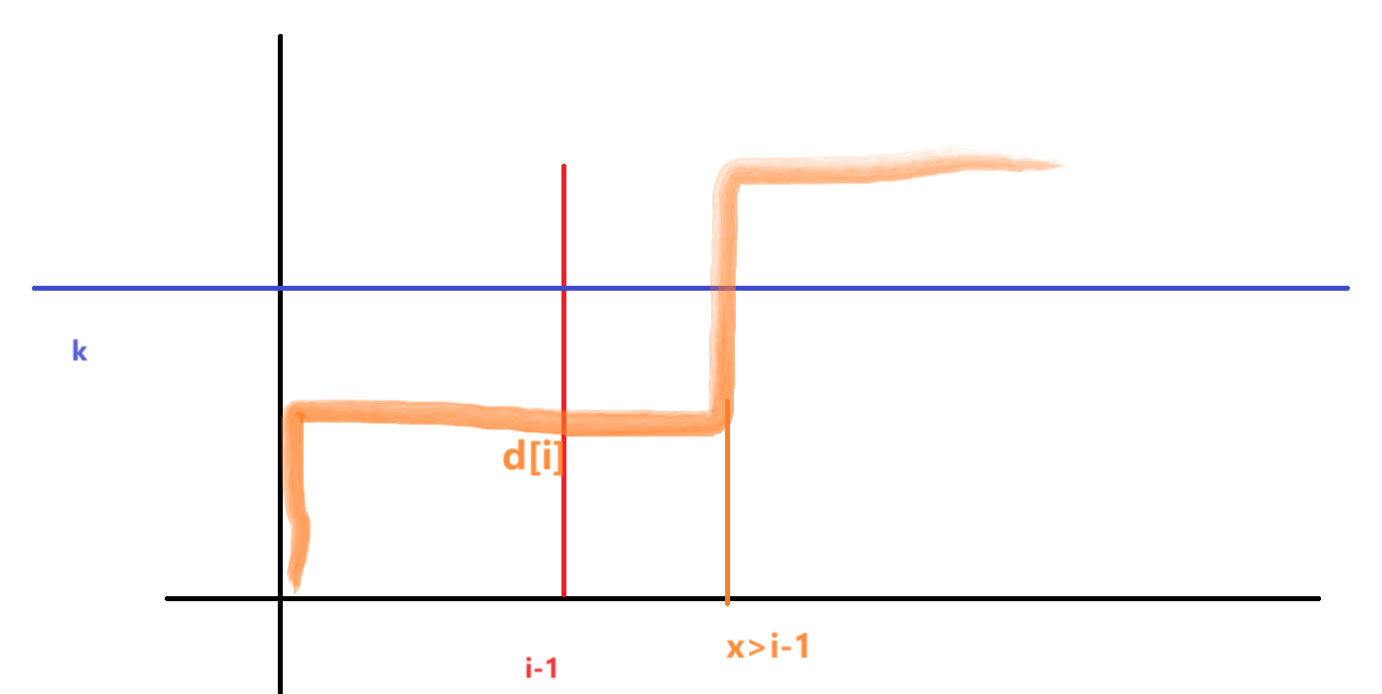
由于 $d_i \in [0,k]$ 所以可以发现当从第 $k$ 行走向 $k+1$ 行的时候，点的横坐标（注意！是横坐标）必定大于 $i-1$。
于是我们转为枚举这个点，$f(n,S,i,k)$ 的组合意义就是 $(0,0) \rightarrow (j,k) \rightarrow (j,k+1) \rightarrow (n-1,S)$ 的方案数（$j \in [i,n]$）。
因此可以重新写出它的表达式：

$$f(n,S,i,k) = \sum\limits_{j=i}^n \binom{j+k}{j} \times \binom{n+S-j-k-2}{S-k-1}$$

于是可以推出它的增量转移式：

$$f(n,S,i+1,k) = f(n,S,i,k) - \binom{i+k}{i} \times \binom{n+s-i-k-2}{S-k-1}$$

有了上述两个增量转移式，就可以增量维护四个 $f$ 函数求答案了。
为了方便再抄一遍：

$$f(n,S,i,k+1)=f(n,S,i,k) + \binom{k+i}{i-1} \times \binom{S-k+n-i-2}{n-i-1}$$

$$f(n,S,i+1,k) = f(n,S,i,k) - \binom{i+k}{i} \times \binom{n+S-i-k-2}{S-k-1}$$

代码

非常的好写））

//题解：https://www.acwing.com/solution/content/247598/

#include <bits/stdc++.h>
using namespace std;
const long long N = 3e6 + 15, mod = 998244353;

long long qmi(long long a, long long k) {
    long long res = 1;
    while (k) {
        if (k & 1) res = (res * 1ll * a) % mod;
        a = (a * 1ll * a) % mod;
        k >>= 1;
    }
    return res;
}

long long fac[N], inv[N];

void init() {
    fac[0] = 1;
    for (long long i = 1; i <= 3000000; i++) fac[i] = (fac[i - 1] * 1ll * i) % mod;
    inv[3000000] = qmi(fac[3000000], mod - 2);
    for (long long i = 2999999; i >= 0; i--) inv[i] = (inv[i + 1] * 1ll * (i + 1)) % mod;
}

long long C(long long n, long long m) {
    return ((long long)fac[n] * 1ll * inv[m] % mod * 1ll * inv[n - m]) % mod;
}

struct F {
    long long n, S, i, k;
    long long res;
    void init(long long a, long long b, long long c, long long d) {
        n = a, S = b, i = c, k = d;
        res = 0;
        for (long long di = 0; di <= k; di++) {
            res = (res + C(di + i - 1, i - 1) * 1ll * C(S + n - di - i - 1, n - i - 1) % mod) % mod;
        }
    }
    void changei(long long x) {
        for (; i < x; i++) {
            res += (mod - C(i + k, i) * C(n + S - i - k - 2, S - k - 1) % mod );
        }
        res %= mod;
    }
    void changek(long long x) {
        for (; k < x; k++) {
            res += C(k + i, i - 1) * C(S - k + n - i - 2, n - i - 1) % mod;
        }
        res %= mod;
    }
} f1, f2, f3, f4;

long long T, n;
long long a[N], c[N], w[N];
long long ans;

int main() {
    init();
    scanf("%lld", &T);
    while (T--) {
        scanf("%lld", &n);
        for (long long i = 1; i <= n; i++) scanf("%lld", &a[i]), c[i] = c[i - 1] + a[i];
        for (long long i = 1; i < n; i++) scanf("%lld", &w[i]);
        ans = 0; long long S = c[n];
        f1.init(n, S, 1, c[1]); f2.init(n, S, 1, S);
        f3.init(n + 1, S - 1, 2, S - 1);
        f4.init(n + 1, S - 1, 2, c[1] - 1);
        for (long long i = 1; i < n; i++) {
            f1.changei(i), f2.changei(i), f3.changei(i + 1), f4.changei(i + 1);
            f1.changek(c[i]), f4.changek(c[i] - 1);
            ans += w[i] * (c[i] * (2ll * f1.res % mod - f2.res + mod) % mod + i * (f3.res - 2 * f4.res + mod) % mod) % mod;
            ans = (ans + mod) % mod;
        }   
        printf("%lld\n", ans);
    }
    return 0;
}