$\Huge\color{orchid}{点击此处获取更多干货}$

记忆化搜索

上帖由于信息节点之间的关联方式形成了高度适配递归方法的树结构，因此引入了递归方法来解决动态规划问题，但动态规划问题存在着另一种更普适的递归方法，即本帖即将介绍的记忆化搜索。递推方法能用的场合它几乎都能用，但它的优势在于当递推方法中的状态难以表示，问题难以求解时，它可以较好的求解。

本问题可以形式化的描述为“在$r$行$c$列的矩阵中可按照上、下、左、右四个方向来移动，求其中最长的下降路径长度”，和之前介绍过的最长上升子序列问题类似，可以用$dp(i,j)$表示移动到位置$(i,j)$时的最长下降路径长度，$dp$图表也可以很容易的给出：

其中四个方向上必须满足递减关系才可转移，并且还可得知：起点周围的值一定都更小，终点周围的值一定都更大，下降路径一定从矩阵中的“极大值点”开始，以“极小值点”结束。那么问题来了：这些极大值点和极小值点分别在哪儿？

虽然有办法找出这些极大值点和极小值点（提高篇FloodFill中会提到），但是如果在$r$行$c$列的矩阵中共找出了$p$个极大值点和$q$个极小值点，那么在状态转移中共要进行$p*q$次转移，每一次的时间复杂度都是$O(r*c)$，那么总时间复杂度可达$O(p*q*r*c)$，其中还涉及了大量重复计算。这么做很显然会导致运算时间的大幅度增长。

因此本帖中不考虑极值点位于何处，而是把矩阵中的每一个位置都视作起点，用递归方式即深度优先搜索（$\text{DFS}$）寻找一下从该位置出发，可以得到的最长下降路径长度，$dp(i,j)$也需要做一些修改，不再表示到达$(i,j)$，而表示从$(i,j)$出发。假如矩阵中存在两个极大值点$(sx_1,sy_1),(sx_2,sy_2)$，从它们开始的下降路径都能经过某个非极值点$(mx,my)$，并可由该位置到达某极小值点$(ex,ey)$，如下图所示：

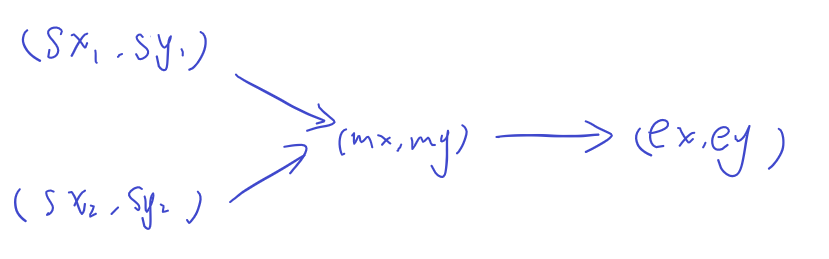
那么从$(sx_1,sy_1)$途经$(mx,my)$到达$(ex,ey)$的过程中，上述三个位置的值都会被更新，与此同时，由于当且仅当周围的值满足递减关系的时候才可转移，因此不存在某一个位置到达极小值点后再回到当前位置的情况，某一个$dp(i,j)$一旦确定就不会再更改。之后以$(sx_2,sy_2)$为起点再次进行转移，路过$(mx,my)$的时候，由于$dp(mx,my)$已经确定，故$dp(mx,my)$不用重复计算，而是可以直接将原值拿来使用。

在对整个矩阵中的所有位置依次递归转移和计算的时候，有可能会出现起点状态的值已经在之前的某次计算中确定的情况，省去了重复计算的时间，可以在$O(r*c)$的时间复杂度之下解决问题。

C++ 代码

#include <iostream>
#include <algorithm>
using namespace std;

int** mat, ** dp;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1}, r, c;

int dfs(int x, int y) {
    int& v = dp[x][y];                  //引用类型，可以同时修改dp表中的值
    if (v != 0) return v;               //非零的状态一定是已经确定了的，不用重复计算
    v = 1;                              //单个位置自身可以构成下降路径，长度至少为1
    for (int i = 0; i < 4; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 0 && nx < r
         && ny >= 0 && ny < c           //未出界，并且周围值更小，才满足转移条件
         && mat[nx][ny] < mat[x][y]) {
            v = max(v, dfs(nx, ny) + 1);//自顶向下递归转移    
        }
    }
    return v;                           //全部转移完毕之后返回
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> r >> c;
    mat = new int*[r];
    dp = new int*[r];
    for (int i = 0; i < r; i++) {
        mat[i] = new int[c];
        for (int j = 0; j < c; j++) {
            cin >> mat[i][j];
        }
        dp = new int[c]();              //空括号new，构造数组同时全部赋值0
    }

    int ans = 0;
    for (int i = 0; i < r; i++) {
        for (int j = 0; j < c; j++) {
            ans = max(ans, dfs(i, j));  //把每个位置视作起点，用递归方法进行状态转移
        }
    }
    cout << ans << endl;

    for (int i = 0; i < r; i++) {
        delete[] mat[i], dp[i];
    }
    delete[] mat, dp;
    return 0;
}