强连通分量（一下简称为块）：任意两点间都存在路径的子图

那么根据块的定义，块中的所有牛都会被整个块的牛认为是受欢迎的

首先用tarjan算法缩点，这样做的好处是图中不再有环

tarjan算法

想清楚了其实不难理解（废话）

就是用dfs加上一个栈，给每个点打上时间戳，

dfn[i]代表i的时间戳，low[i]代表从i往下dfs的所有点中最小的时间戳

如果处理完后仍有low[i]=dfn[i]，那么i下面一定挂着一个块

以这幅图为例，圈起来的是块，3和4自成一个块

不难发现块头节点都满足dfn[i]=low[i]（其实是我懒得写证明了）

void tarjan(int u){
    dfn[u]=low[u]=++nowt;   //打时间戳
    stk[++tt]=u,st[u]=1;    //入栈
    for(int i=h[u];~i;i=ne[i]){
        int v=to[i];
        if(!dfn[v]){    //未遍历过的点
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(st[v])  //遍历过且还在栈中的点（成环边，例如上图中2到1的边）
            low[u]=min(low[u],dfn[v]);
        //遍历过且不在栈中的点和u没有任何关系，例如上图中1到3的边
    }
    if(low[u]<dfn[u])
        return;
    //u下面挂着一个块
    int v;
    do{
        v=stk[tt--],st[v]=0,merge(v,u); //并查集合并
    }while(v!=u);
}

后续处理

现在我们已经得到了一个有很多块，没有环的图

（因为所有环都成为了某个块的一部分）

原问题于是变成了所有块中是否有且仅有一个汇点

因为没有环，所以不可能没有汇点

如果有多于一个汇点，如下图，答案一定为0

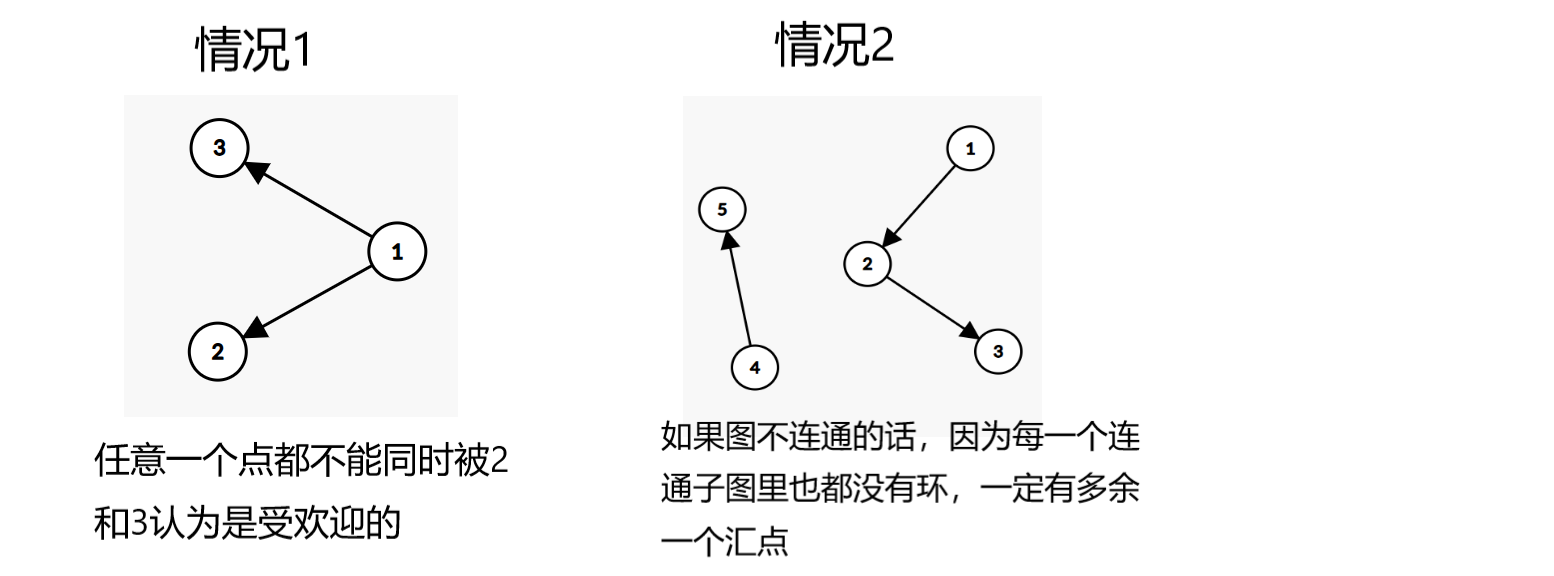
排除掉答案为0的情况之后，数一数汇点那个块里包含多少牛就行了

完整代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=10010,M=50010;
int from[M],to[M],ne[M],h[N],idx;
int dfn[N],low[N],nowt;
int fa[N];
int eout[N];
int stk[N],tt;
bool st[N];
inline void add(int a,int b){   //加边
    from[idx]=a,to[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int find(int x){    //并查集找根
    if(fa[x]!=x)
        fa[x]=find(fa[x]);
    return fa[x];
}
inline void merge(int a,int b){ //并查集合并
    int x=find(a),y=find(b);
    if(x==y)
        return;
    fa[y]=x;
}
void tarjan(int u){ //tarjan缩点
    dfn[u]=low[u]=++nowt;
    stk[++tt]=u,st[u]=1;
    for(int i=h[u];~i;i=ne[i]){
        int v=to[i];
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(st[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(low[u]<dfn[u])
        return;
    int v;
    do{
        v=stk[tt--],st[v]=0,merge(v,u);
    }while(v!=u);
}
int main(){
    memset(h,-1,sizeof h);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)   //初始化并查集
        fa[i]=i;
    for(int i=1;i<=m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
    }
    for(int i=1;i<=n;i++)   //缩点
        if(!dfn[i])
            tarjan(i);
    for(int i=0;i<idx;i++){ //遍历所有边
        int x=find(from[i]),y=find(to[i]);
        if(x!=y)    //记录x的出度
            eout[x]++;
    }
    int block=0,res=0;
    for(int i=1;i<=n;i++)
        if(!eout[find(i)]){ //出度为0的点就是汇点
            if(block&&block!=find(i)){  //有多于一个汇点
                printf("0");
                return 0;
            }
            res++,block=find(i);    //数点数
        }
    printf("%d",res);
    return 0;
}