算法分析

规则后的图形

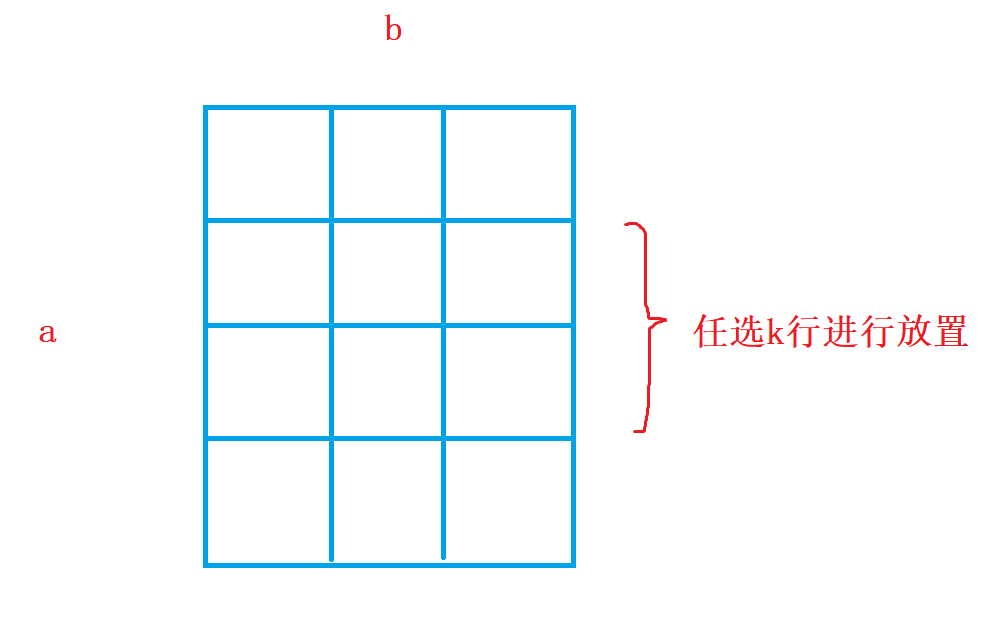
题目给定的图片是不规则图形，我们可以将它分解成若干个规则图形，因为规则图形可以通过公式直接计算出来，如上图所示，对于某个规则的矩形，长度是a，宽度是b，放k辆车（k <= b <= a），在长度是a行中任选k行进行摆放，共有b列，第一辆车有b种摆放方案，第二辆车有b - 1中摆放方案…，第k辆车有b - k + 1种摆放方案，因此一共有$C_a^kA_b^k$种摆放方案

分解图形（按照红线位置划分成两个矩形）

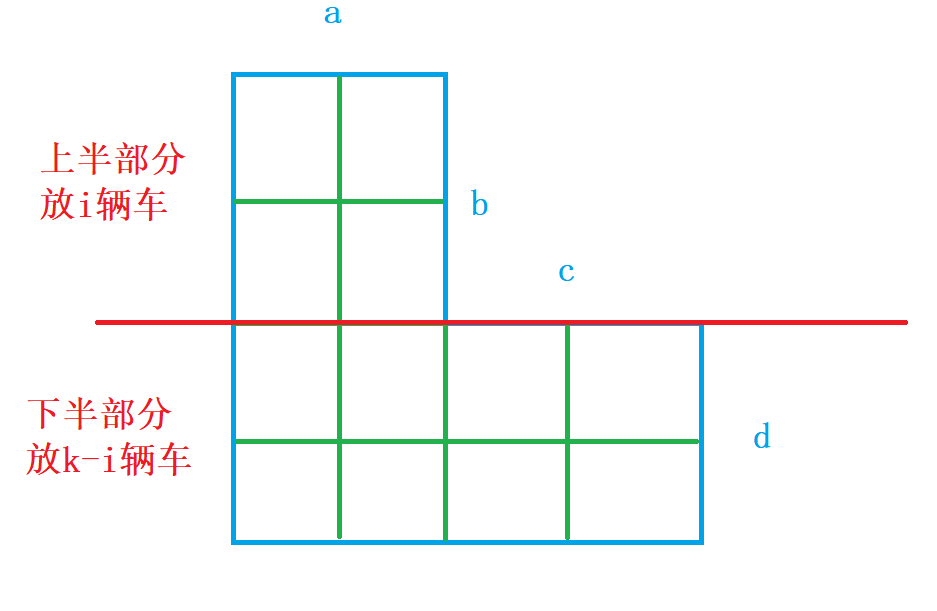
上半部分摆放i辆车，有 $C_b^iA_a^i$ 种摆放方案

下半部分摆放k - i辆车，由于上半部分摆放了i辆车，占用的列对下半部分选择有了一定的影响，即占用的列对于下半部分是不可使用的，因此从d行中选k - i行，有a + c - i列可以进行摆放并摆放k - i辆车，因此有 $C_d^{k - i}A_{a + c - i}^{k - i}$ 种摆放方案

由于上半部分的摆放情况 和 下半部分的摆放情况是相互独立的，因此可以使用乘法原理，上半部分摆放i辆车，整张图的摆放方案是 $C_b^iA_a^iC_d^{k - i}A_{a + c - i}^{k - i}$

时间复杂度 $O(Nlogmod)$

N = 2000，mod = 100003

参考文献

算法提高课

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 2010, mod = 100003;
    static long[] fact = new long[N];
    static long[] infact = new long[N];
    static long qmi(int a, int k, int p)
    {
        long res = 1 % p;
        long t = a;
        while(k != 0)
        {
            if((k & 1) == 1) res = res * t % mod;
            k >>= 1;
            t = t * t % mod;
        }
        return res;
    }
    static long C(int a, int b)
    {
        if(a < b) return 0;
        return fact[a] * infact[b] % mod * infact[a - b] % mod;
    }
    static long P(int a, int b)
    {
        if(a < b) return 0;
        return fact[a] * infact[a - b] % mod;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);

        fact[0] = infact[0] = 1;
        for(int i = 1;i < N - 1;i ++)
        {
            fact[i] = fact[i - 1] * i % mod;
            infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
        }

        int a = scan.nextInt();
        int b = scan.nextInt();
        int c = scan.nextInt();
        int d = scan.nextInt();
        int k = scan.nextInt();

        long res = 0;
        for(int i = 0;i <= k;i ++)
        {
            res = (res + C(b, i) * P(a, i) % mod * C(d, k - i) * P(a + c - i, k - i) % mod) % mod;
        }

        System.out.println(res);
    }
}