$\Huge\color{orchid}{点击此处获取更多干货}$

递归法动态规划

之前说过，动态规划既可以用递归法也可以用递推法来实现，在之前的各种问题中大量使用递推法，是因为状态之间的转移关系不太复杂，且大多数基于线性的序列式数据结构（数组，矩阵）。那么当动态规划问题基于的是适用递归的关联式结构（树、图），或状态之间的递推式转移关系难以表示，那么递归方法就成为首选了。本问题的情况属于前一种。

按照问题描述和样例，所有员工的人物关系可以抽象为如下图所示的有向树结构：

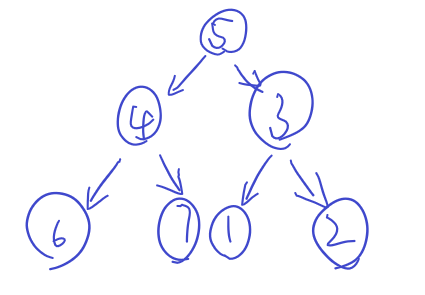
图中每个节点代表一个员工，该树结构的根节点是节点5，每个节点的权值都是1。那么本问题可以形式化为“在树结构中选择若干不相邻的节点，得到最大的节点权值之和”。以其中一条链5->3->2为例，当第2层的节点2被选中时，第1层的节点3是不能被选的，那么最多只能再考虑第0层的节点5，此时可以认为选择节点2时的结果是由节点5的状态转移而来的；当节点2不被选中时，节点3可以考虑，那么不选择节点2的结果是由节点3的状态转移而来的。但是这种思路会带来一个无法解决的问题：有向树结构中，如何从最下层的叶子节点反向访问其上2层的节点？

由此可以确定，自底向上的方法行不通，那么用自顶向下的方式考虑一下。此处的出发点不再是“从根节点到某一个节点的路径上”，而是“以某一个节点为根的子树中”。并且，选择根节点时，它的后继节点都不能选择，但是它后继节点的子树不受影响，而每个节点都只有选或不选两种状态，因此状态值也对应的有2种，即“在以该节点为根的子树中，选/不选该节点时能得到的最大节点权值之和”，可以分别用$sel(i)$和$lev(i)$分别对应选$\text{（select，选出）}$节点$i$和不选$\text{（leave，留下）}$节点$i$。回到之前的用例，树结构的根是节点5，其中能获得的最大节点权值和就是$max\{sel(5),lev(5)\}$。当5被选了之后，其后继节点3、4都不能再选了，因此$sel(5)=1+lev(3)+lev(4)$，其中1是节点5的权值；当5未被选择时，后继节点3、4都有选与不选2种情况，因此$lev(5)=max\{sel(3),lev(3)\} + max\{sel(4),lev(4)\}$。由此，可以得到转移关系，以及dp图表：

搜索状态的时候需要递归，状态之间的转移仍然是递推式的，在回溯的过程中完成。

C++ 代码

#include <iostream>
#include <algorithm>
using namespace std;

int tot = 1, * fin, * last, * pre;  //树结构使用图结构的方式存储
int* happy;                         //happy就是员工的快乐值，节点的权值
int* sel, * lev;                    //分别对应选与不选（选出与留下）
bool* hasPrev;                      //用来找根节点，无前驱的就是

void connect(int s, int e) {
    fin[tot] = e;
    pre[tot] = last[s];
    last[s] = tot++;
}

void dfs(int cur) {
    sel[cur] += happy[cur];         //选择当前节点，先累加节点权值
    for (int i = last[cur]; i != 0; i = pre[i]) {
        int child = fin[i];
        dfs(child);                 //向下递归搜索每一个后继节点
        sel[cur] += lev[child];     //回溯的过程中完成转移
        lev[cur] += max(sel[child],lev[child]);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    fin = new int[n];               //树边一共就n-1条
    last = new int[n + 1]();        //节点序号从1开始
    pre = new int[n];
    happy = new int[n + 1];
    sel = new int[n + 1]();
    lev = new int[n + 1]();
    hasPrev = new bool[n + 1]();
    for (int i = 1; i <= n; i++) cin >> happy[i];
    for (int i = 1; i < n; i++) {
        int e, s;
        cin >> e >> s;              //输入是反向的，根节点在后面
        connect(s, e);
        hasPrev[e] = true;
    }
    int root;
    for (int i = 1; i <= n; i++) {
        if (!hasPrev[i]) {          //无前驱即为根节点
            root = i;
            break;
        }
    }
    dfs(root);
    cout << max(sel(root), lev(root)) << endl;
    delete[] fin, last, pre, sel, lev, happy, hasPrev;
    return 0;
}