思路

首先，中心一定存在。其次，只有一个中心的情况是平凡的，考虑存在多个中心的情况。

1. 若存在两个中心 $x, y$，则它们必是父子（直接相连）。否则选择它们中间的任意顶点 $v$，可以发现切除 $x$ 或 $y$ 后的最大连通块比切除 $v$ 后的最大连通块大，即切除 $v$ 更优，这与 $x, y$ 是中心矛盾。证明如下：
   
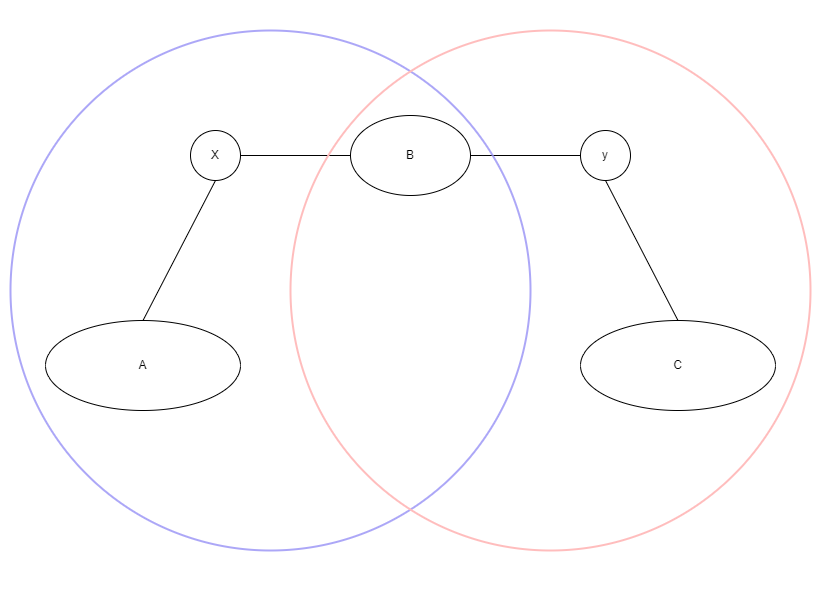
   如图所示，$x, y$ 是树的中心，$B$ 是 $x, y$ 之间的连通块，$A$ 是以 $x$ 为根的子树往下的最大连通块，$C$ 是以 $y$ 为根的子树往下的最大连通块。

   1. 连通块大小 $sz(A) = sz(C)$。假设 $sz(A) \ne sz(C)$，不妨设 $sz(A) > sz(C)$，则图中紫色圈大于红色圈。则切除 $x$ 后，最大连通块大小等于 $max(sz(A), sz(红色圈))$。切除 $y$ 后，最大连通块大小等于 $max(sz(C), sz(紫色圈)) = sz(紫色圈)$。由于 $x, y$ 都是中心，因此 $max(sz(A), sz(红色圈)) = sz(紫色圈)$，因此 $sz(红色圈) = sz(紫色圈)$，因此 $sz(A) = sz(C)$，这与 $sz(A) > sz(C)$ 矛盾。
   2. 选择连通块 $B$ 中与 $x$ 相连的点 $z$，切除 $z$ 后，最大连通块大小为 $max(sz(A) + 1, sz(红色圈) - 1)$，而切除 $x$ 后，最大连通块大小等于 $max(sz(A), sz(红色圈)) = sz(红色圈) = sz(紫色圈) > max(sz(A) + 1, sz(红色圈) - 1)$，因此切割 $z$ 更优。

2. 若存在两个中心 $x, y$，不妨设 $x$ 是 $y$ 的父亲，则以 $y$ 为根的子树大小 $sz(y)$ 必然为 $\frac{n}{2}$（相当于上图中去掉连通块 $B$ 后，紫色圈大小仍然等于红色圈）。反证：假设 $sz(y) < \frac{n}{2}$，则断开 $x, y$ 之间的边可把整棵树分成两棵子树，分别以 $x$ 和 $y$ 为根，将它们记为 $T_x, T_y$，满足 $sz(T_x) > \frac{n}{2}, sz(T_y) < \frac{n}{2}$。因此，在原树上，将 $y$ 切除后最大连通块是 $T_x$，而将 $x$ 切除后最大连通块要么是 $T_y$，要么是 $T_x$ 的子树，无论如何大小都小于 $sz(T_x)$，即切除 $x$ 比切除 $y$ 更优，这与它们都是中心矛盾。同理，若 $sz(y) > \frac{n}{2}$，则切除 $y$ 比切除 $x$ 更优。

3. 若存在两个中心 $x, y$，不妨设 $x$ 是 $y$ 的父亲，将 $y$ 的一个叶节点切除后与 $x$ 相连，$x$ 就会变成唯一中心。证明：切割并重新连接后 $sz(T_y) = \frac{n}{2} - 1, sz(T_x) = \frac{n}{2} + 1$，由性质 $2$，切除 $y$ 或 $y$ 子树上的任意节点获得的最大连通块不小于 $sz(T_x)$，即大于 $\frac{n}{2}$；切除 $x$ 后获得的最大连通块一定小于 $sz(T_x)$，小于等于 $\frac{n}{2}$；切除新加的叶节点后获得的最大连通块显然大于 $\frac{n}{2}$；切除 $x$ 子树上的除了新加叶节点外的任意节点获得的每个连通块的大小，与这棵树被改变前切除它们获得的每个连通块的大小相同，因此最大连通块大小都大于 $\frac{n}{2}$。因此 $x$ 是唯一中心。
4. 不可能存在两个以上中心。假设存在两个以上中心，对于其中的任意三个，由性质 $1$，它们必然构成完全图进而形成环，这与树中无环矛盾。

时间复杂度 $O(n)$。

#include <iostream>
#include <vector>

#define endl "\n"

using namespace std;
using G = vector<vector<int>>;

int n;

int dfs(int u, int p, G &g, vector<int> &c, int &mxsz) {
  int sz = 1, mx = 0;
  for (auto son : g[u])
    if (son != p) {
      int t = dfs(son, u, g, c, mxsz);
      mx = max(mx, t);
      sz += t;
    }
  mx = max(mx, n - sz);
  if (mx <= mxsz) {
    if (mx < mxsz) c.clear();
    c.push_back(u);
    mxsz = mx;
  }
  return sz;
}

int leaf(int u, int p, G &g) {
  for (auto son : g[u])
    if (son != p)
      return leaf(son, u, g);
  return u;
}

void solve() {
  cin >> n;
  G g(n + 1, vector<int>());
  for (int i = 0, x, y; i < n - 1; i++) {
    cin >> x >> y;
    g[x].push_back(y);
    g[y].push_back(x);
  }

  vector<int> centroids;
  int mxsz = n;
  dfs(1, -1, g, centroids, mxsz);

  if (centroids.size() == 1) {
    int a = centroids[0];
    int b = g[a][0];
    cout << a << " " << b << " " << endl;
    cout << a << " " << b << " " << endl;
  } else {
    int a = centroids[0], b = centroids[1];
    int lf = leaf(a, b, g);
    cout << g[lf][0] << " " << lf << " " << endl;
    cout << b << " " << lf << " " << endl;
  }
}

int main() {
  cin.tie(0)->sync_with_stdio(0);
  int t;
  cin >> t;
  while (t--) solve();
  return 0;
}