题目描述

给你一个 n 个节点的无向带权图，节点编号为 0 到 n - 1。图中总共有 m 条边，用二维数组 edges 表示，其中 edges[i] = [a_i, b_i, w_i] 表示节点 a_i 和 b_i 之间有一条边权为 w_i 的边。

对于节点 0 为出发点，节点 n - 1 为结束点的所有最短路，你需要返回一个长度为 m 的 boolean 数组 answer，如果 edges[i] 至少 在其中一条最短路上，那么 answer[i] 为 true，否则 answer[i] 为 false。

请你返回数组 answer。

注意，图可能不连通。

样例

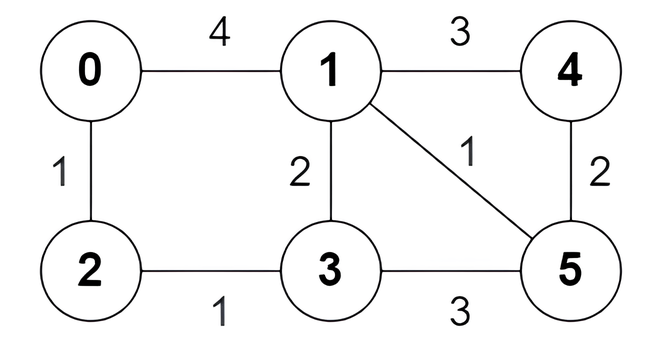
输入：n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

输出：[true,true,true,false,true,true,true,false]

解释：

以下为节点 0 出发到达节点 5 的 所有 最短路：

路径 0 -> 1 -> 5：边权和为 4 + 1 = 5。
路径 0 -> 2 -> 3 -> 5：边权和为 1 + 1 + 3 = 5。
路径 0 -> 2 -> 3 -> 1 -> 5：边权和为 1 + 1 + 2 + 1 = 5。

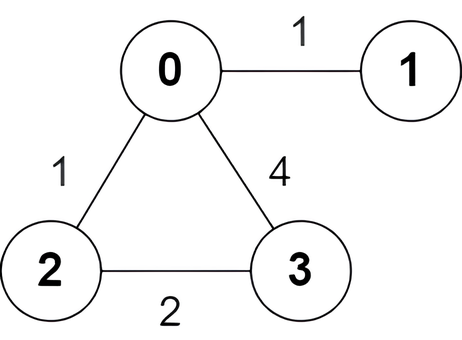
输入：n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

输出：[true,false,false,true]

解释：

只有一条从节点 0 出发到达节点 3 的最短路 0 -> 2 -> 3，边权和为 1 + 2 = 3。

限制

• 2 <= n <= 5 * 10^4
• m == edges.length
• 1 <= m <= min(5 * 10^4, n * (n - 1) / 2)
• 0 <= a_i, b_i < n
• a_i != b_i
• 1 <= w_i <= 10^5
• 图中没有重边。

算法1

(图论，最短路) $O((n + m) \log n)$

1. 可以通过强制使用这条边来判断一条边是否在 $0$ 到 $n - 1$ 的最短路。
2. 通过堆优化 Dijkstra 算法求出从 $0$ 出发的单源最短路和 $n - 1$ 出发的单源最短路。
3. 枚举每条边 $(u, v, w)$，判断 $d_0(u) + w + d_1(v)$ 或者 $d_0(v) + w + d_1(u)$ 是否等于从 $0$ 到 $n - 1$ 的最短路。

时间复杂度

• 堆优化 Dijkstra 算法的时间复杂度为 $O((n + m) \log n)$。
• 枚举判断答案的时间复杂度为 $O(m)$。
• 故总时间复杂度为 $O((n + m) \log n)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储邻接表和最短路的数据结构。

C++ 代码

#define LL long long

class Solution {
private:
    void dij(int st, int n, vector<LL> &dis,
        const vector<vector<pair<int, int>>> &graph
    ) {
        priority_queue<pair<int, int>> heap;
        heap.emplace(st, 0);

        dis.resize(n, INT64_MAX);
        dis[st] = 0;

        while (!heap.empty()) {
            auto t = heap.top();
            heap.pop();
            int u = t.first, d = -t.second;

            if (d > dis[u])
                continue;

            for (const auto &[v, w] : graph[u])
                if (dis[v] > dis[u] + w) {
                    dis[v] = dis[u] + w;
                    heap.emplace(v, -dis[v]);
                }
        }
    }

public:
    vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
        const int m = edges.size();

        vector<LL> d1, d2;
        vector<vector<pair<int, int>>> graph(n);

        for (const auto &e : edges) {
            graph[e[0]].emplace_back(e[1], e[2]);
            graph[e[1]].emplace_back(e[0], e[2]);
        }

        dij(0, n, d1, graph);
        dij(n - 1, n, d2, graph);

        vector<bool> ans(m, false);

        if (d1[n - 1] == INT64_MAX)
            return ans;

        for (int i = 0; i < m; i++) {
            int u = edges[i][0], v = edges[i][1], w = edges[i][2];
            if (d1[u] == INT64_MAX || d1[v] == INT64_MAX
            || d2[u] == INT64_MAX || d2[v] == INT64_MAX)
                continue;

            if (d1[u] + w + d2[v] == d1[n - 1] || d1[v] + w + d2[u] == d1[n - 1])
                ans[i] = true;
        }

        return ans;
    }
};

算法2

(图论，最短路，BFS/DFS) $O((n + m) \log n)$

1. 通过堆优化 Dijkstra 算法求出从 $0$ 出发的单源最短路。
2. 从终点出发开始广度优先或者深度优先遍历，对于当前节点 $v$，以及连接的边 $(u, w)$，如果 $dis(v) = dis(u) + w$，则说明这条边在以 $0$ 为起点的最短路上，且 $v$ 到 $n$ 也存在一条最短路（经过的边都是按照这个规则遍历得到），所以 $(v, u, w)$ 这条边就一定在 $0$ 到 $n - 1$ 的最短路上。

时间复杂度

• 堆优化 Dijkstra 算法的时间复杂度为 $O((n + m) \log n)$。
• 逆序遍历的时间复杂度为 $O(n + m)$。
• 故总时间复杂度为 $O((n + m) \log n)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储邻接表和最短路的数据结构。

C++ 代码

#define LL long long

class Solution {
private:
    void dij(int st, int n, vector<LL> &dis,
        const vector<vector<tuple<int, int, int>>> &graph
    ) {
        priority_queue<pair<int, int>> heap;
        heap.emplace(st, 0);

        dis.resize(n, INT64_MAX);
        dis[st] = 0;

        while (!heap.empty()) {
            auto t = heap.top();
            heap.pop();
            int u = t.first, d = -t.second;

            if (d > dis[u])
                continue;

            for (const auto &[v, w, _] : graph[u])
                if (dis[v] > dis[u] + w) {
                    dis[v] = dis[u] + w;
                    heap.emplace(v, -dis[v]);
                }
        }
    }

public:
    vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
        const int m = edges.size();

        vector<LL> dis;
        vector<vector<tuple<int, int, int>>> graph(n);

        for (int i = 0; i < m; i++) {
            const auto &e = edges[i];
            graph[e[0]].emplace_back(e[1], e[2], i);
            graph[e[1]].emplace_back(e[0], e[2], i);
        }

        dij(0, n, dis, graph);

        vector<bool> ans(m, false);

        if (dis[n - 1] == INT64_MAX)
            return ans;

        queue<int> q;
        vector<bool> vis(n, false);

        q.push(n - 1);
        vis[n - 1] = true;

        while (!q.empty()) {
            int v = q.front();
            q.pop();

            for (const auto &[u, w, id] : graph[v]) {
                if (dis[v] < dis[u] + w)
                    continue;

                ans[id] = true;

                if (!vis[u]) {
                    q.push(u);
                    vis[u] = true;
                }
            }
        }

        return ans;
    }
};