题目描述

难度分:$1800$

输入$n(1 \leq n \leq 2 \times 10^5)$和一个长为$n$的数组$a(1 \leq a[i] \leq 10^9)$。

有$n$个盛水的容器，从上到下串起来，从上到下第$i$个容器的容量为$a[i]$。初始时，所有容器都是空的。

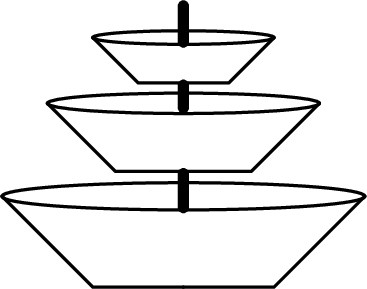
然后输入$m(1 \leq m \leq 2 \times 10^5)$个询问，每个询问的格式如下（$i$从$1$开始）：

1. 1 i x，表示往第$i$个容器倒$x(1 \leq x \leq 10^9)$ 单位的水。溢出的水会流到下一个容器，下一个容器溢出的水会流到下下一个容器，……，最后一个容器溢出的水会流到地板上。
2. 2 i，输出第$i$个容器有多少单位的水。

输入样例$1$

2
5 10
6
1 1 4
2 1
1 2 5
1 1 4
2 1
2 2

输出样例$1$

4
5
8

输入样例$2$

3
5 10 8
6
1 1 12
2 2
1 1 6
1 3 2
2 2
2 3

输出样例$2$

7
10
5

算法

并查集

刚开始用线段树来模拟的，大概思路是第$i$个杯子上面所有水的体积超出所有杯子体积的部分就是流到第$i$个杯子中的水体积。但是提交上去之后WA第$3$个$case$，仔细分析后发现有点问题。因为假设$i$上面有个杯子$j$满了，需要向下流水，而$j$位置的水是不能补到上面去的，因此如果$j$上面不是所有杯子都满了，留到下面去的水会更多，所以这个思路是错的。

思考良久发现还可以用并查集来模拟，用一个$O(n)$规模的数组$v$来记录每个杯子中水的体积。如果第$i$个杯子满了，就让它与下一个杯子连成一个整体，即让并查集的$find(i)$指向$i$下面最近的那个没满的杯子。

这样一来，只要加入路径压缩，倒水操作就可以在均摊$O(logn)$级别的常数操作下更新本次倒水所要更新的杯子。

而对于查询操作：

1. 如果$find(i)=i$，说明当前杯子没满，打印当前杯子中水的体积。
2. 否则说明当前杯子已经满了，打印当前杯子的体积。

复杂度分析

时间复杂度

初始化并查集的时间复杂度为$O(n)$。而每个询问都至少需要操作一次并查集，为了考虑到定向，并查集只加入了路径压缩，并未使用按秩合并来优化，所以操作的时间复杂度是$O(logn)$级别，询问的总时间复杂度为$O(mlogn)$。

综上，算法整体的时间复杂度为$O(n+mlogn)$。

空间复杂度

并查集$find$操作的空间需要递归$O(logn)$层，但是并查集数组的规模是$O(n)$，因此瓶颈在于并查集数组。因此，算法的额外空间复杂度为$O(n)$。

C++ 代码

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int N = 200010;
int n, m, a[N], p[N];
LL v[N];

int find(int x) {
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void merge(int x, int y) {
    int rx = find(x), ry = find(y);
    if(rx != ry) {
        p[rx] = ry;
    }
}

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        p[i] = i;
        v[i] = 0;
    }
    p[n + 1] = n + 1;
    v[n + 1] = 0;     // 地面
    scanf("%d", &m);
    for(int index = 1; index <= m; index++) {
        int tp, i, x;
        scanf("%d", &tp);
        if(tp == 1) {
            scanf("%d%d", &i, &x);
            int j = find(i);
            v[j] += x;
            while(j <= n && v[j] >= a[j]) {
                LL remain = v[j] - a[j];
                v[find(j + 1)] += remain;
                merge(j, find(j + 1));
                j = find(j + 1);
            }
        }else {
            scanf("%d", &i);
            if(find(i) != i) {
                printf("%lld\n", a[i]);      // 当前杯子的水已经满了
            }else {
                printf("%lld\n", v[i]);      // 当前杯子没满
            }
        }
    }
    return 0;
}