题目描述

难度分:$1600$

输入$n(1 \leq n \leq 2 \times 10^5)$，$k(n \leq k \leq 10^9)$和长为$n$的数组 $a(1 \leq a[i] \leq 2 \times 10^5)$。

每次操作，你可以选择一个整数$x$，把所有大于$x$的$a[i]$都减小至 $x$，花费为减少量之和，要求单次操作的花费不能超过$k$。

要使所有$a[i]$都一样，最少要操作多少次？

输入样例$1$

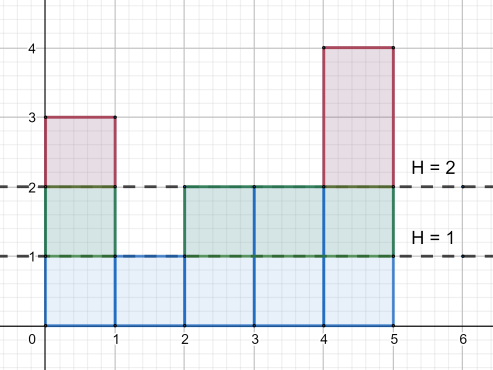
5 5
3 1 2 2 4

输出样例$1$

2

输入样例$2$

4 5
2 3 4 5

输出样例$2$

2

算法

贪心

比较容易发现的是，最终数组的所有值都会变成$min(h)$，因此先将$h$降序排列，从前往后贪心。当遍历到$i$位置时，假设前面的$i-1$个数已经变成了$h[i-1]$，要想把$i-1$个$h[i-1]$变成$i-1$个$h[i]$需要付出代价$(i-1) \times (h[i-1]-h[i])$，假设前面$(i-1)$个数变成$h[i-1]$的代价为$cost$，则分为以下两种情况：

1. $cost+(i-1) \times (h[i-1]-h[i]) \leq k$，游刃有余，可以用一次操作将前$i-1$个数变成$h[i]$。将代价$cost$累加上$(i-1) \times (h[i-1]-h[i])$，继续检查后面的。
2. $cost+(i-1) \times (h[i-1]-h[i]) \gt k$，没办法一次操作把前$i-1$个数变成$h[i]$，只能先用一次操作把前$i-1$个数减少$\lfloor \frac{k-cost}{i-1} \rfloor$（其中$\lfloor . \rfloor$表示对$.$向下取整）得到$d$。考虑到$k$的代价能将$i-1$个相同的数降低$t=\lfloor \frac{k}{i-1} \rfloor$个单位，因此再将$d$操作$t$次变成$d-t$。这样一来，遍历到$i+1$位置时，要将前$i$个数变成$h[i]$代价就是$d \% t \times (i-1)$。

需要注意的是，如果遍历完数组后$cost \gt 0$，就还需要一次操作。

复杂度分析

时间复杂度

瓶颈在于排序，排序完后遍历一遍数组就能得到答案，时间复杂度为$O(nlog_2n)$。

空间复杂度

除了输入的$h$数组，仅使用了有限几个变量，因此空间复杂度就是排序的空间复杂度，以快排为基准，额外空间复杂度为$O(log_2n)$。

C++ 代码

#include <bits/stdc++.h>
 
using namespace std;
typedef long long LL;

const int N = 200010;
int n, k, h[N];

int main() {
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &h[i]);
    }
    sort(h + 1, h + n + 1);
    reverse(h + 1, h + n + 1);
    LL cost = 0, ans = 0;
    for(int i = 2; i <= n; i++) {
        LL delta = h[i - 1] - h[i];
        if(cost + (i - 1) * delta >= k) {
            delta -= (k - cost) / (i - 1);
            ans += 1 + delta / (k / (i - 1));
            cost = delta % (k / (i - 1)) * (i - 1);
        }else {
            cost += (i - 1) * delta;
        }
    }
    if(cost > 0) ans++;
    printf("%lld\n", ans);
    return 0;
}

附上一版初始代码，本质上是一样的，但由于每次给定一个$x$会“削弱”一类数，所以用一个$map$去重是更加理所当然的思路。唯一不同的是这个代码里用了有序表（用哈希表也可以，但是后面要排序，不会影响时间复杂度）去重，空间复杂度是$O(n)$的。

先用一个有序表对$h$数组去重计数，然后将有序表展开成一个二元组（数值，频数）数组$tup$，$tup$按照数值大小升序排列，从后往前贪心（降序排列也可以，贪心方向相反）。

维护$sufsum$，$sufcnt$和$ans$，前两个变量表示比$tup[i].first$大的元素之和、元素个数，$ans$为答案。当遍历到$num=tup[i].first$，$freq=tup[i].second$时，有两种情况：

1. $sufsum-freq \times num \lt k$，能够通过一次操作将比$num$大的数全部削成$num$，暂时不做操作数的结算，更新$sufsum=sufsum+freq \times num$，$sufcnt=sufcnt+freq$继续遍历下一个二元组。
2. $sufsum-freq \times num \geq k$，这样能够把大于$num$的数经过一次操作削成$target=\lceil \frac{sufsum-k}{sufcnt} \rceil$，其中$\lceil . \rceil$表示对$.$向上取整。然后尝试继续削$target$，$k$次操作能够把$sufcnt$个$target$削减$delta=\lfloor \frac{k}{sufcnt} \rfloor$，一共可以操作$times=\lfloor \frac{target-num}{delta} \rfloor$次。因此，最终大于$num$的数会被削成$target-times \times delta$，更新$sufsum=sufcnt \times (target-times \times delta) + freq \times num$和$sufcnt=sufcnt+freq$继续遍历下一个二元组。

注意在遍历完$tup$数组后，如果$sufsum \gt n \times min(h)$，说明还没有达成所有数都一样的成就，还需要进行一次操作。

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

const int N = 200010;
int n, k, h[N];

int main() {
    scanf("%d%d", &n, &k);
    map<int, int> counter;
    for(int i = 1; i <= n; i++) {
        scanf("%d", &h[i]);
        counter[h[i]]++;
    }
    vector<PII> tup;
    for(auto&[num, freq]: counter) {
        tup.push_back({num, freq});
    }
    LL sufsum = 0, sufcnt = 0, ans = 0;
    for(int i = tup.size() - 1; i >= 0; i--) {
        LL num = tup[i].first, freq = tup[i].second;
        LL cost = sufsum - sufcnt*num;
        if(cost >= k) {
            int target = (sufsum - k + sufcnt - 1) / sufcnt;
            ans++;
            int delta = k / sufcnt, times = (target - num) / delta;
            ans += times;
            sufsum = sufcnt*(target - times*delta) + freq*num;
        }else {
            sufsum += 1LL*freq*num;
        }
        sufcnt += freq;
    }
    LL mn = tup[0].first;
    if(sufsum > n*mn) ans++;
    printf("%lld\n", ans);
    return 0;
}