1047. 糖果

题目描述

由于在维护世界和平的事务中做出巨大贡献，Dzx被赠予糖果公司2010年5月23日当天无限量糖果免费优惠券。

在这一天，Dzx可以从糖果公司的 $N$ 件产品中任意选择若干件带回家享用。

糖果公司的 $N$ 件产品每件都包含数量不同的糖果。

Dzx希望他选择的产品包含的糖果总数是 $K$ 的整数倍，这样他才能平均地将糖果分给帮助他维护世界和平的伙伴们。

当然，在满足这一条件的基础上，糖果总数越多越好。

Dzx最多能带走多少糖果呢？

注意：Dzx只能将糖果公司的产品整件带走。

输入格式

第一行包含两个整数 $N$ 和 $K$。

以下 $N$ 行每行 $1$ 个整数，表示糖果公司该件产品中包含的糖果数目，不超过 $1000000$。

输出格式

符合要求的最多能达到的糖果总数，如果不能达到 $K$ 的倍数这一要求，输出 $0$。

数据范围

$1 \le N \le 100$,
$1 \le K \le 100$,

输入样例：

5 7
1
2
3
4
5

输出样例：

14

样例解释

Dzx的选择是2+3+4+5=14，这样糖果总数是7的倍数，并且是总数最多的选择。

算法

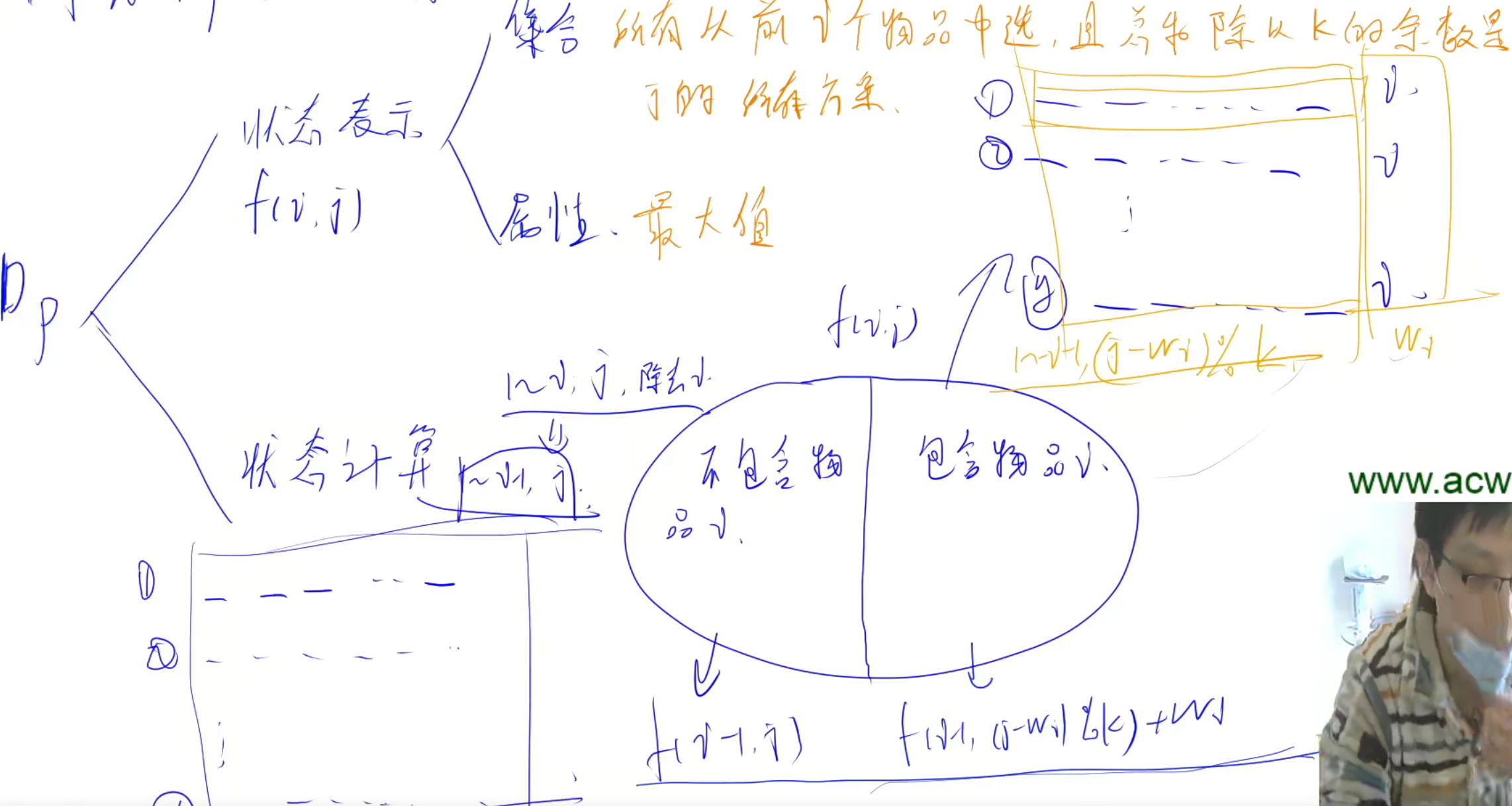
时间复杂度

$O(nk)$

代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 105;

int n, k;
int w[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &k);

    for(int i = 1; i <= n; i ++)
        scanf("%d", &w[i]);

    // 初始化f[0]：由于只有 f[0][0] 是有意义/合法的（初值为 0），f[1...k - 1]都是无意义的/非法的（初值为 -INF）
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;

    for(int i = 1; i <= n; i ++)
        for(int j = 0; j < k; j ++)
            f[i][j] = max(f[i - 1][j], f[i - 1][((j - w[i]) % k + k) % k] + w[i]);

    printf("%d", f[n][0]);
    return 0;
}