一种基于蒙的思路

题目描述

有一长方形，长为 343720 单位长度，宽为 233333 单位长度。在其内部左上角顶点有一小球（无视其体积），其初速度如图所示且保持运动速率不变，分解到长宽两个方向上的速率之比为 dx : dy = 15 :17。小球碰到长方形的边框时会发生反弹，每次反弹的入射角与反射角相等，因此小球会改变方向且保持速率不变（如果小球刚好射向角落，则按入射方向原路返回）。从小球出发到其第一次回到左上角顶点这段时间里，小球运动的路程为多少单位长度？答案四舍五入保留两位小数。

思路

为什么会有思路的呢，我猜的
这个算法的正确率从理论上来看是1/2
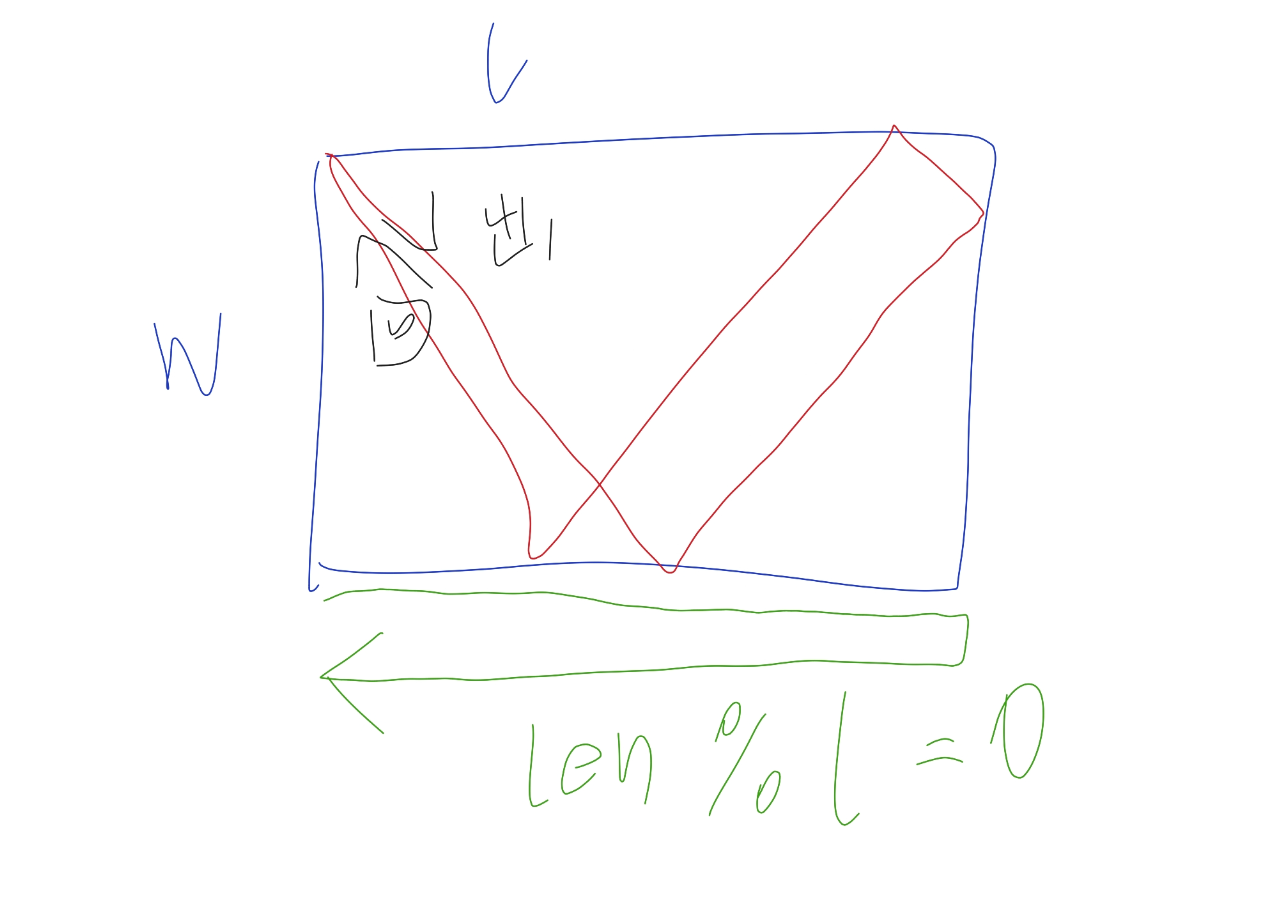
从下图来看，设射线在横轴走的路程为len，方块长为l，高为w
则如果射线回到左上角的点或者右上角的点时有：(所以正确率是1/2)
len必然可以整除l，也就是找len%l=0的点
所以我们可以直接开个while(len%l>=1e-9)来求

2.实际上这个思路漏洞百出，还得是蒙的，因为换成整型 如下图就不对了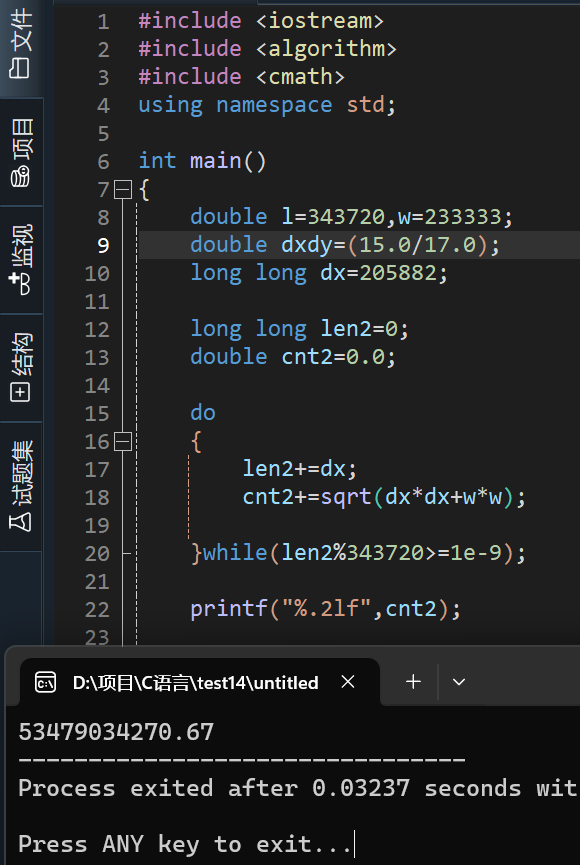

C++ 代码

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

int main()
{
    double l=343720,w=233333;
    double dxdy=(15.0/17.0);
    double cnt=0.0,len=0.0;
    do{
        len+=w*dxdy;
        cnt+=sqrt(w*dxdy*w*dxdy+w*w);
    }while((double)((int)len%(int)l)>=1e-9);

    printf("%.2lf\n",cnt);
}