题目描述

在有向图 G
中，每条边的长度均为 1
，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1．路径上的所有点的出边所指向的点都直接或间接与终点连通。
2．在满足条件 1
的情况下使路径最短。

注意：图 G
中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入格式
第一行有两个用一个空格隔开的整数 n
和 m
，表示图有 n
个点和 m
条边。

接下来的 m
行每行 2
个整数 x、y
，之间用一个空格隔开，表示有一条边从点 x
指向点 y
。

最后一行有两个用一个空格隔开的整数 s、t
，表示起点为 s
，终点为 t
。

输出格式
输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。

如果这样的路径不存在，输出 −1
。

数据范围
0<n≤10000
,
0<m≤200000
,
0<x,y,s,t≤n,s≠t

样例

这是我们学校选拔赛的一道题，赛时没跳出来，后来也花了很多时间才完全调出来，于是想写自己的第一篇正式题解，也因为临近蓝桥杯而耽搁
来分析这道题目
1．路径上的所有点的出边所指向的点都直接或间接与终点连通。
2．在满足条件 1
的情况下使路径最短。
条件1可以用dfs爆搜判断点是否能到终点，再用for循环遍历每个点的出边，判断该点所指向的点都是否直接或间接与终点连通
条件2则是在我们求出满足条件的所有点后按照符合条件的走出一条正确道路
故采取dfs+bfs的处理
1.采取保留父节点的dfs形式，很快发现会导致死循环
2.采取标记走过点的dfs形式，

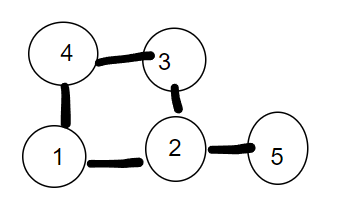
比如这里从1走到5，1 2 5和1 4 3 2 5这两条路径都可以到，但因为2先被标记，所以走不到第二条路径上，我们就需要刷新标记数组，从每个点遍历，也就是仅仅一次dfs无法找出所有点，需要每个点都d一遍，已经判断完成可以continue；最终就能判断出所有能到终点的点

后续遍历每个点的出边即可，记得考虑最后一个节点的问题
再接着bfs即可求出最短路径
样例解释

如上图所示，满足条件的路径为1->3->4->5。注意点2不能在答案路径中，因为点2连了一条边到点6，而点6不与终点5连通。
部分解释在代码中，200多ms就跑过了

#include <bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N=10010,M=200010;
int h[N],e[M],ne[M],idx;
int n,m,s,t;
int dist[N];
int st[N],vis[N],ch[N];//st数组记录该点是否满足条件，vis记录是否到过这个点， ch记录这个点是不是可以到终点 
void add(int a,int b)
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
void dfs(int u)//优化dfs
{
    if(u==t)
    {
        ch[u]=1;
        vis[u]=1;
    }
    vis[u]=1;

    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(vis[j])
        {
            if(ch[j])
            {
                ch[u]=1;
                break;
            }else
            {
                continue;
            }
        }
        dfs(j);
        if(ch[j]==1)
        {
            ch[u]=1;
            break;
        }
    }

}
int bfs(int u)
{
    queue<int> q;
    q.push(u);
    memset(dist,-1,sizeof dist);
    dist[u]=0;
    while(q.size())
    {
        int tt=q.front();
        q.pop();
        for(int i=h[tt];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(st[j]==0||dist[j]!=-1)
            {
                continue;
            }
            dist[j]=dist[tt]+1;
            q.push(j);
        }
    }
    return dist[t];
}
signed main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    cin>>s>>t;
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof vis);
        if(ch[i])
        {
            continue;
        }
        dfs(i);
    }//ch数组处理完毕
    for(int i=1;i<=n;i++)
    {
        st[i]=1;
    }
    // for(int i=1;i<=n;i++)
    // {
    //     cout<<ch[i]<<" ";
    // }

    for(int i=1;i<=n;i++)
    {
        int flag=0;
        for(int j=h[i];j!=-1;j=ne[j])
        {
            flag=1;
            int k=e[j];
            // if(i==2&&k==6)
            // {
            //     cout<<ch[6]<<endl;
            // }
            if(ch[k]==0)
            {
                st[i]=0;
            }

        }
        if(flag==0&&i!=t)
        {
            st[i]=0;
        }//考虑最后一个节点，如果他都没有出边，自然标记为0

    }
//     for(int i=1;i<=n;i++)
//     {
//      cout<<st[i]<<" ";
//  }
    //再来一遍bfs求最短路径
    int ans=bfs(s);
    if(ans<0||st[s]==0)//如果我起点都不满足条件，那就直接gg
    {
        cout<<-1<<endl;
    }else
    {
        cout<<ans<<endl;
    }
    return 0;

}