题目描述

给你一个二维数组 edges 表示一个 n 个点的无向图，其中 edges[i] = [u_i, v_i, length_i] 表示节点 u_i 和节点 v_i 之间有一条需要 length_i 单位时间通过的无向边。

同时给你一个数组 disappear，其中 disappear[i] 表示节点 i 从图中消失的时间点，在那一刻及以后，你无法再访问这个节点。

注意，图有可能一开始是不连通的，两个节点之间也可能有多条边。

请你返回数组 answer，answer[i] 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点 i，那么 answer[i] 为 -1。

样例

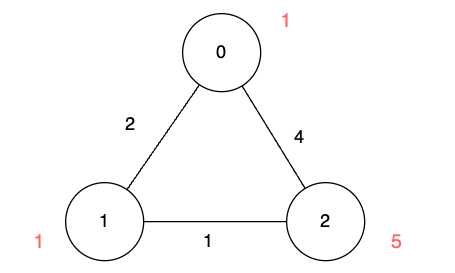
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]

输出：[0,-1,4]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

对于节点 0，我们不需要任何时间，因为它就是我们的起点。
对于节点 1，我们需要至少 2 单位时间，通过 edges[0] 到达。
    但当我们到达的时候，它已经消失了，所以我们无法到达它。
对于节点 2，我们需要至少 4 单位时间，通过 edges[2] 到达。

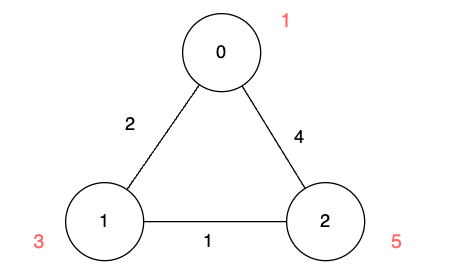
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]

输出：[0,2,3]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

对于节点 0，我们不需要任何时间，因为它就是我们的起点。
对于节点 1，我们需要至少 2 单位时间，通过 edges[0] 到达。
对于节点 2，我们需要至少 3 单位时间，通过 edges[0] 和 edges[1] 到达。

输入：n = 2, edges = [[0,1,1]], disappear = [1,1]

输出：[0,-1]

解释：

当我们到达节点 1 的时候，它恰好消失，所以我们无法到达节点 1。

限制

• 1 <= n <= 5 * 10^4
• 0 <= edges.length <= 10^5
• edges[i] == [u_i, v_i, length_i]
• 0 <= u_i, v_i <= n - 1
• 1 <= length_i <= 10^5
• disappear.length == n
• 1 <= disappear[i] <= 10^5

算法

(最短路) $O((n + m) \log n)$

1. 使用堆优化的 Dijkstra 算法求解单源最短路。
2. 每次拓展时，如果目标节点会在最短时间下消失，则不进行松弛更新。

时间复杂度

• 堆优化 Dijkstra 算法的时间复杂度为 $O((n + m) \log n)$。其中 $m$ 为边的数量。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储图邻接表，堆，和距离数组。

C++ 代码

class Solution {
public:
    vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
        vector<vector<pair<int, int>>> graph(n);

        for (const auto &e : edges) {
            graph[e[0]].emplace_back(e[1], e[2]);
            graph[e[1]].emplace_back(e[0], e[2]);
        }

        priority_queue<pair<int, int>> heap;
        vector<int> dis(n, INT_MAX);

        dis[0] = 0;
        heap.push(make_pair(0, 0));

        while (!heap.empty()) {
            auto t = heap.top();
            heap.pop();

            int u = t.second, d = -t.first;
            if (d > dis[u])
                continue;

            for (const auto &v : graph[u]) {
                int vd = dis[u] + v.second;
                if (vd < disappear[v.first] && dis[v.first] > vd) {
                    dis[v.first] = vd;
                    heap.push(make_pair(-vd, v.first));
                }
            }
        }

        for (int i = 0; i < n; i++)
            if (dis[i] == INT_MAX)
                dis[i] = -1;

        return dis;
    }
};