题目描述

给你一个二维整数数组 point，其中 points[i] = [x_i, y_i] 表示二维平面内的一个点。同时给你一个整数 w。你需要用矩形 覆盖所有 点。

每个矩形的左下角在某个点 (x_1, 0) 处，且右上角在某个点 (x_2, y_2) 处，其中 x_1 <= x_2 且 y_2 >= 0，同时对于每个矩形都 必须 满足 x_2 - x_1 <= w。

如果一个点在矩形内或者在边上，我们说这个点被矩形覆盖了。

请你在确保每个点都 至少 被一个矩形覆盖的前提下，最少 需要多少个矩形。

注意：一个点可以被多个矩形覆盖。

样例

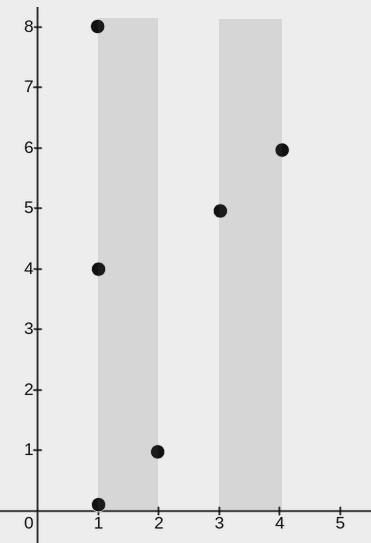
输入：points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1

输出：2

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (1, 0)，右上角在 (2, 8)。
一个矩形的左下角在 (3, 0)，右上角在 (4, 8)。

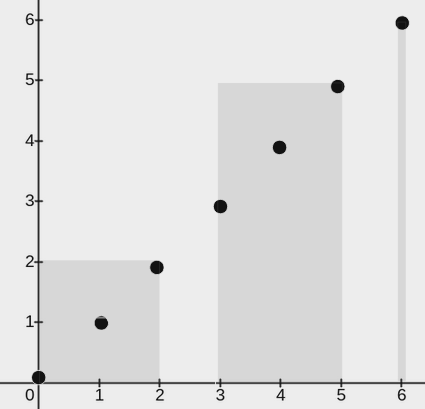
输入：points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2

输出：3

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (0, 0)，右上角在 (2, 2)。
一个矩形的左下角在 (3, 0)，右上角在 (5, 5)。
一个矩形的左下角在 (6, 0)，右上角在 (6, 6)。

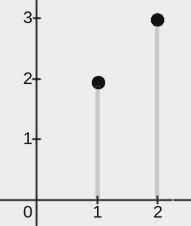
输入：points = [[2,3],[1,2]], w = 0

输出：2

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (1, 0)，右上角在 (1, 2)。
一个矩形的左下角在 (2, 0)，右上角在 (2, 3)。

限制

• 1 <= points.length <= 10^5
• points[i].length == 2
• 0 <= x_i == points[i][0] <= 10^9
• 0 <= y_i == points[i][1] <= 10^9
• 0 <= w <= 10^9
• 所有点坐标 (x_i, y_i) 互不相同。

算法

(排序，贪心) $O(n \log n)$

1. 只关心横坐标，将所有点按照横坐标从小到大排序。
2. 遍历排序后的横坐标，放置长度为 w 的线段覆盖住所有的横坐标。对于当前位置的坐标，如果其与坐标起点的差值大于 w，则新开一个矩形。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 排序后，遍历数组一次。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(\log n)$ 的额外空间存储排序的系统栈。

C++ 代码

class Solution {
public:
    int minRectanglesToCoverPoints(vector<vector<int>>& points, int w) {
        sort(points.begin(), points.end());

        const int n = points.size();

        int ans = 1;
        for (int i = 0, j = 0; i < n; i++)
            if (points[i][0] - points[j][0] > w) {
                ++ans;
                j = i;
            }

        return ans;
    }
};