$\Huge\color{orchid}{点击此处获取更多干货}$

状态压缩+动态规划

将$n*m$的矩形划分为若干$1*2$的小矩形，从“划分”的角度不容易找解决方法，可以反过来从“摆放”的角度来看，即“在$n*m$的矩形棋盘上摆放若干$1*2$的小矩形，并且能不多不少的覆盖住整个棋盘”。就“摆放”的方向而言，小矩形可以有水平和竖直两种方向，同时考虑这两种方向也不容易得出解法，因此我们可以优先考虑其中一种方向，比如先尝试将小矩形按水平方向摆放到棋盘上，这样的话当小矩形不能再按水平方向摆放上棋盘时，竖直方向的摆放方式也就确定了。

还有一个值得留意的地方是，如果在某列的某个位置水平摆放一个小矩形，那么下一列同一行的位置有可能就不能再摆放了，因此可以看成是“在某一列中水平摆放的小矩形会影响下一列的摆放情况”，那么就可以用一个参数$i$来表示已经全部被覆盖的棋盘列数，但是为了方便转移还得表示出第$i+1$列有哪些已经在之前的摆放中被占用，这需要用和棋盘行数相同的多个参数来表示。如果把这些参数的值用数组下标来表示，且不说管理$dp$表的时候$new$和$delete$都要调用好多次，在枚举状态的时候也不太方便。并且这些参数无非就代表着第$i+1$列各个位置是“被占用”还是“空闲”两种状态，如果用一个整数的二进制位来表示这些状态，那么对于状态的表示和枚举来说，都会方便很多。

综上所述，$dp$图表如下：

（写错了，$k$应该是可以转移到$j$的状态，而不是由$j$转移到的状态）

状态之间能够互相转移，前提条件是这样的状态是允许出现的，而在该问题中，不是$0\sim 2^i-1$之间所有的状态都允许出现，因为上文中提到的摆放方式中本身就包含了一条规则，即先放水平方向再放竖直方向之后，前$i$列的所有位置都不重不漏的被覆盖，那么按照水平方向在前$i$列摆放完所有的矩形之后，第$i+1$列中出现的每一段连续空闲位置，其长度都必须是偶数，即代表了用于表示每个状态的j，其二进制位中只能出现偶数个连续的0。比如$j=10011B$就是允许出现的，而$j=10101B$就是不允许出现的。

还剩下一个关键问题：怎样的$k$代表的状态，可以转移到$j$的状态？

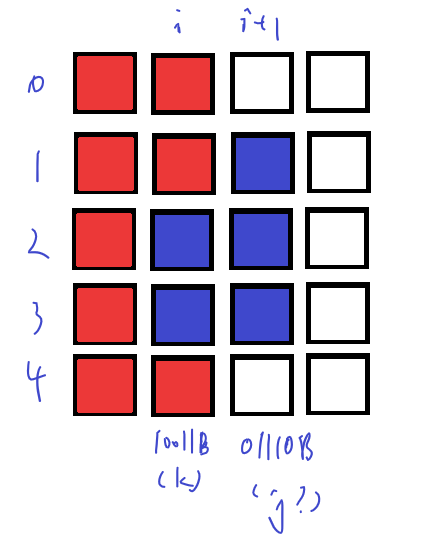
如图所示，假设我们按照水平优先的方式摆完前$i-1$列后，$i$列上已被占用的位置构成了二进制数$k=10011B$，那么在$i$列也摆放完毕后，$i+1$列上被占用的位置能否构成$j=01110B$呢？显然不行，因为$i$列$1$行已经由于前$i-1$列的摆放而被占用，故在该位置水平摆放小矩形，使得$i+1$列$1$行被占用构成$01110B$是行不通的，因此$k$状态能转移到$j$状态的条件就是$k$和$j$相同位阶的数位中不能同时出现1，即按位相与后所得结果的任意二进制位不能是1($k~and~j == 0$)

C++ 代码

主程序：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 12, M = 1 << N;   //测试环境不允许new/delete，需要利用一下n,m的上限11

size_t dp[N][M];
bool st[M];                     //用来表示每个状态是否允许存在

size_t countMethods(int n, int m);

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m;
    while (true) {
        cin >> n >> m;
        try {
            cout << countMethods(n, m) << endl;
        }
        catch (logic_error e) {
            break;
        }
    }
    return 0;
}

方案数：

/**
* @brief 求划分方案总数
* @param n,m 矩形棋盘的行、列数
* @return 方案总数
* @warning n,m必须非0，否则需要抛出异常
*/
size_t countMethods(int n, int m) {
    if (n == 0 || m == 0) {
        throw logic_error("error");         //主函数的try块捕获到此异常时就结束运行
    }
    memset(dp, 0, sizeof(dp));              //dp表已在全局区定义，可以直接用sizeof
    for (int i = 0; i < (1 << n); i++) {    //二进制中1左移i位就代表了十进制中的2^i
        st[i] = 1;
        int cnt = 0;                        //此处统计的是连续0的个数
        for (int j = 0; j < n; j++) {
            if ((i >> j) & 1) {             //二进制位中遇到0就累加，遇到1就停止
                if (cnt & 1) {              //连续0的个数为奇数，意味着此状态不允许出现
                    st[i] = 0;
                    cnt = 0;
                }
            }
            else {
                cnt++;
            }
        }
        if (cnt & 1) {                      //尾端的连续0也需要判断
            st[i] = 0;
        }
    }

    dp[0][0] = 1;                           //什么都没摆放也算一种
    for (int i = 1; i <= m; i++) {
        for (int j = 0; j < (1 << n); j++) {
            for (int k = 0; k < (1 << n); k++) {
                if ((k & j) == 0 && st[j | k]) {
                    /*
                    * 解释一下j|k
                    * 在水平摆放阶段，可能占用第i列空闲位置的方式有两种
                    * 一种是摆在第i-1列的小矩形横向占用了第i列同一行的空闲位置（由k产生）
                    * 另一种是在i列继续摆放小矩形时本身就占用了空闲位置（由此产生了j）
                    * 两种情况都考虑上，那就成了j|k，在这个状态下需要保证不出现奇数个连续0
                    */
                    dp[i][j] += dp[i-1][k]; 
                }
            }
        }
    }
}