$\Huge\color{orchid}{点击此处获取更多干货}$

动态规划（递推）

用动态规划方法解决整数划分问题，既可以用自底向上的递推方法，也可以用自顶向下的递归方法。本帖先介绍递推方法，此方法类似于背包问题。某一种划分中的每一个数都可以视作背包问题中$v=w$的物品，在背包问题中$dp(i,j)$表示的状态为在前$i$个物品中选，总体积不超过$j$。此问题中仍然可以使用$dp(i,j)$，表示的状态是从$1\sim i$中选数，其总和等于$j$。由于并未限制这些数的选取次数，因此可以用完全背包问题的类似方法解决，先给出原始的$dp$图表：

选$i$的情况也可以类似的用$dp(i,j-i)$代替，原因如下：

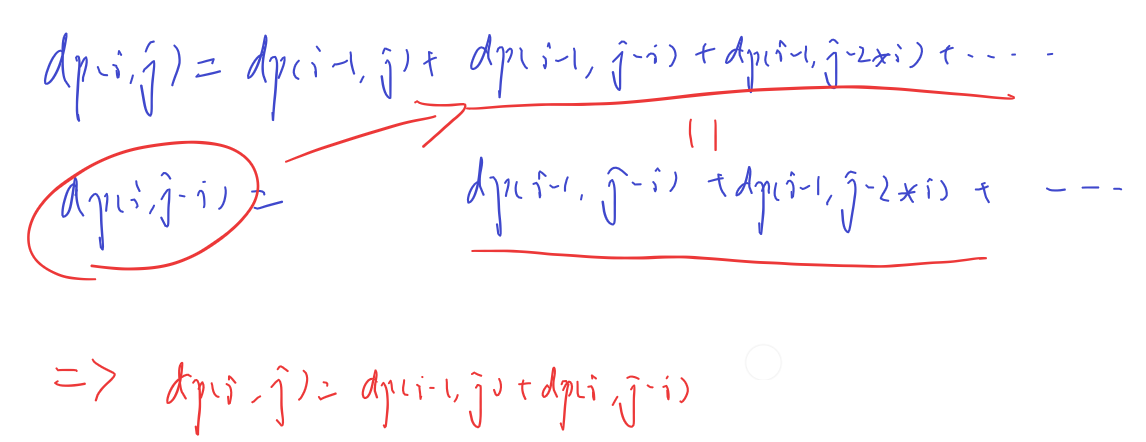
同样，$dp(i,x)$只能从$dp(i-1,x)$得出，因此可以用一维$dp$表来记录。枚举顺序和完全背包问题一致

C++ 代码

#include <iostream>
using namespace std;

const int MOD = 1e9 + 7;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int* dp = new int[n + 1]();
    dp[0] = 1;                      //什么都不选视作1种方案

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= n; j++) {
            if (j >= i) {
                dp[j] = (dp[j] + dp[j - i]) % MOD;
            }
        }
    }
    cout << dp[n] << endl;
    delete[] dp;
    return 0;
}