题目描述

给定一个链表，如果存在环，则返回环的入口；否则返回null。

注意：请不要修改链表。

进一步：能否只是用额外 $O(1)$ 的空间？

算法

(链表，快慢指针扫描) $O(n)$

本题的做法比较巧妙。
用两个指针 $first, second$ 分别从起点开始走，$first$ 每次走一步，$second$ 每次走两步。
如果过程中 $second$ 走到null，则说明不存在环。否则当 $first$ 和 $second$ 相遇后，让 $first$ 返回起点，$second$ 待在原地不动，然后两个指针每次分别走一步，当相遇时，相遇点就是环的入口。

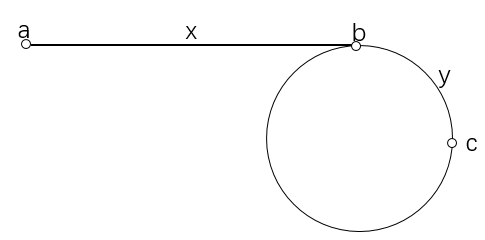
证明：如上图所示，$a$ 是起点，$b$ 是环的入口，$c$ 是两个指针的第一次相遇点，$ab$ 之间的距离是 $x$，$bc$ 之间的距离是 $y$。
则当 $first$ 走到 $b$ 时，由于 $second$ 比 $first$ 多走一倍的路，所以 $second$ 已经从 $b$ 开始在环上走了 $x$ 步，可能多余1圈，距离 $b$ 还差 $y$ 步（这是因为第一次相遇点在 $b$ 之后 $y$ 步，我们让 $first$ 退回 $b$ 点，则 $second$ 会退 $2y$ 步，也就是距离 $b$ 点还差 $y$ 步）；所以 $second$ 从 $b$ 点走 $x + y$ 步即可回到 $b$ 点，所以 $second$ 从 $c$ 点开始走，走 $x$ 步即可恰好走到 $b$ 点，同时让 $first$ 从头开始走，走 $x$ 步也恰好可以走到 $b$ 点。所以第二次相遇点就是 $b$ 点。

另外感谢@watay147提供的另一种思路，可以用公式来说明：$a, b, c, x, y$ 的含义同上，我们用 $z$ 表示从 $c$ 点顺时针走到 $b$ 的距离。则第一次相遇时 $second$ 所走的距离是 $x + (y + z) * n + y$, $n$ 表示圈数，同时 $second$ 走过的距离是 $first$ 的两倍，也就是 $2(x + y)$，所以我们有 $x + (y + z) * n + y = 2(x + y)$，所以 $x = (n - 1) \times (y + z) + z$。那么我们让 $second$ 从 $c$ 点开始走，走 $x$ 步，会恰好走到 $b$ 点；让 $first$ 从 $a$ 点开始走，走 $x$ 步，也会走到 $b$ 点。

时间复杂度分析：$first$ 总共走了 $2x + y$ 步，$second$ 总共走了 $2x + 2y + x$ 步，所以两个指针总共走了 $5x + 3y$ 步。由于当第一次 $first$ 走到 $b$ 点时，$second$ 最多追一圈即可追上 $first$，所以 $y$ 小于环的长度，所以 $x+y$ 小于等于链表总长度。所以总时间复杂度是 $O(n)$。

C++ 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (!head || !head->next) return 0;
        ListNode *first = head, *second = head;

        while (first && second)
        {
            first = first->next;
            second = second->next;
            if (second) second = second->next;
            else return 0;

            if (first == second)
            {
                first = head;
                while (first != second)
                {
                    first = first->next;
                    second = second->next;
                }
                return first;
            }
        }

        return 0;
    }
};