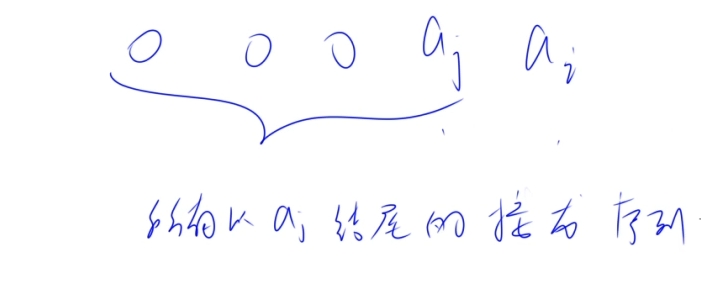题目描述

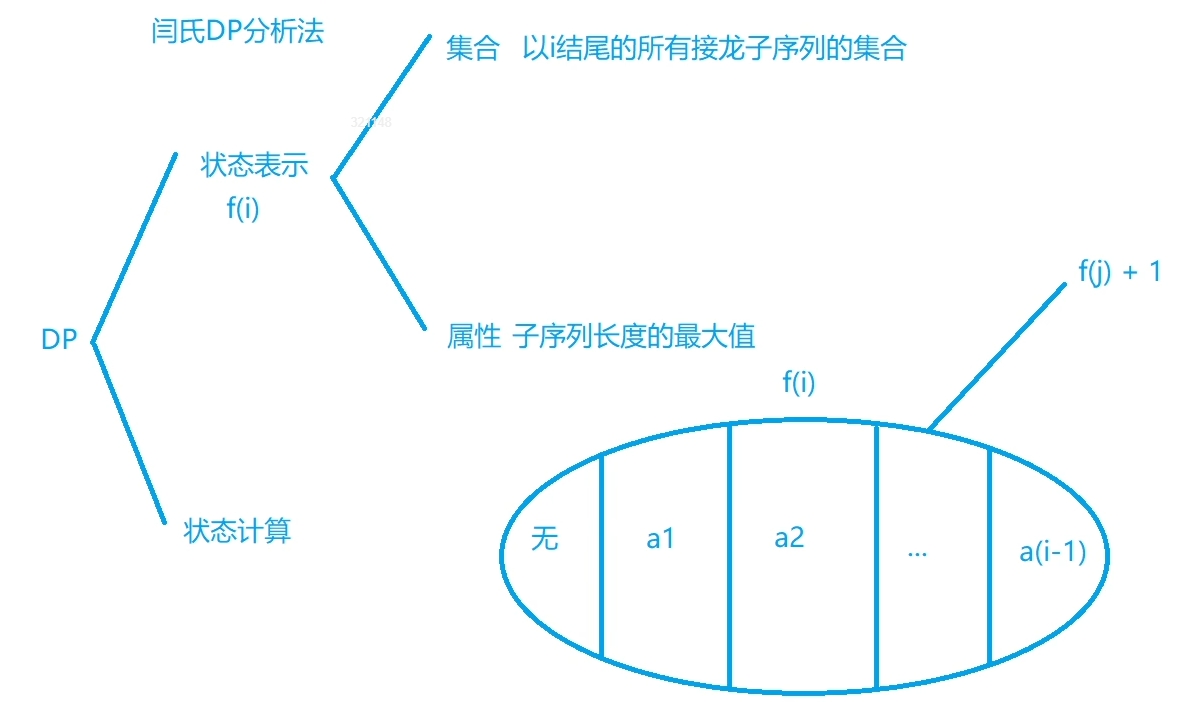
线性DP(类似最长上升子序列)

线性DP

import java.util.*;

public class Main {
    static int N = (int)1e5 + 10;

    static int f[] = new int[N];
    static int a[] = new int[N];
    static int b[] = new int[N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        sc.nextLine();

        for (int i = 1; i <= n; i++)
        {
            String str = sc.next();
            a[i] = Integer.parseInt(str.substring(0,1));
            b[i] = Integer.parseInt(str.substring(str.length() - 1,str.length()));
        }

        //遍历n次,为了能算出从1到i的f[i]
        for (int i = 1; i <= n; i++)
        {
            f[i] = 1;

            //遍历到第i个数字之前
            for (int j = 1; j <= i - 1; j++)
            {
                if (b[j] == a[i]) 
                f[i] = Math.max(f[i], f[j] + 1);
            }
        }

        int res = 0;
        for (int i = 1; i <= n; i++)
            res = Math.max(res, f[i]);

        System.out.println(n - res);


        sc.close();
    }
}

优化线性DP

import java.util.*;

public class Main {
    static int N = (int)1e5 + 10;

    static int f[] = new int[N];
    static int a[] = new int[N];
    static int b[] = new int[N];
    static int g[] = new int [10];//用于存储第i个数字之前以末尾数字k(0 <= k <= 9)为结尾的接龙序列的max
    //即g[k]表示在第i个数字以前,为k为末尾的接龙序列的最大长度


    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        sc.nextLine();

        for (int i = 1; i <= n; i++)
        {
            String str = sc.next();
            a[i] = Integer.parseInt(str.substring(0,1));
            b[i] = Integer.parseInt(str.substring(str.length() - 1,str.length()));
        }

        //遍历n次,为了能算出从1-i的f[i]
        for (int i = 1; i <= n; i++)
        {
            f[i] = 1;

            //由于第i个数字的首位为a[i],那么只关心以a[i]为结尾的数字
            f[i] = Math.max(f[i], g[a[i]] + 1);

            //由于第i个数字的末尾为b[i],那么就要更新g[b[i]
            g[b[i]] = Math.max(g[b[i]], f[i]);

        }


        int res = 0;
        for (int i = 1; i <= n; i++)
            res = Math.max(res, f[i]);

        System.out.println(n - res);


        sc.close();
    }
}