LeetCode 143. Reorder List

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

LeetCode 143. Reorder List 原题链接中等

作者：

yxc , 2018-05-31 15:33:43 , 所有人可见 , 阅读 3458

8

3

题目描述

给定一个链表 $L: L_0→L_1→…→L_{n-1}→L_n$，将它变成 $L_0→L_n→L_1→L_{n-1}→L_2→L_{n-2}→…$
你不能改变节点的值，只能改变节点的指针。

样例1

给定 1->2->3->4, 变成 1->4->2->3。

样例2

给定 1->2->3->4->5, 变成 1->5->2->4->3。

算法

(链表，模拟) $O(n)$

假设初始的链表是 $L_1 \xrightarrow{} L_2 \xrightarrow{} L_3 \xrightarrow{} … \xrightarrow{} L_n$。

分两步处理：

将后半段的指针都反向，变成：$L_1 \xrightarrow{} L_2 \xrightarrow{} L_3 \xrightarrow{} … \xrightarrow{} L_{\lceil n/2 \rceil} \xleftarrow{} L_{\lceil n/2 \rceil+1} \xleftarrow{} … \xleftarrow{} L_n$;
用两个指针分别从1和n开始往中间扫描，将后半段交替插入到前半段，变成：$L_1 \xrightarrow{} L_n \xrightarrow{} L_2 \xrightarrow{} L_{n-1} \xrightarrow{} …$;

时间复杂度分析：整个链表总共扫描三次，第一次求总长度，第二次将后半段反向，第三次将后半段交替插入前半段，所以总时间复杂度是 $O(n)$。

C++ 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void reorderList(ListNode* head) {
        int n = 0;
        for (ListNode *p = head; p; p = p->next) n ++ ;
        if (n <= 2) return;
        ListNode *later = head;
        for (int i = 0; i + 1 < (n + 1) / 2; i ++ )
            later = later->next;
        ListNode *a = later, *b = later->next;

        while (b)
        {
            ListNode *c = b->next;
            b->next = a;
            a = b;
            b = c;
        }

        later->next = 0;
        while (head && head != a)
        {
            b = a->next;
            a->next = head->next;
            head->next = a;
            head = head->next->next;
            a = b;
        }
    }
};

4 评论

有心人 2021-06-28 15:04

这道题目我的思路和y总讲解的不一样，感觉自己的更清晰易懂一些。

# 题目

#### 143. 重排链表

# 思路

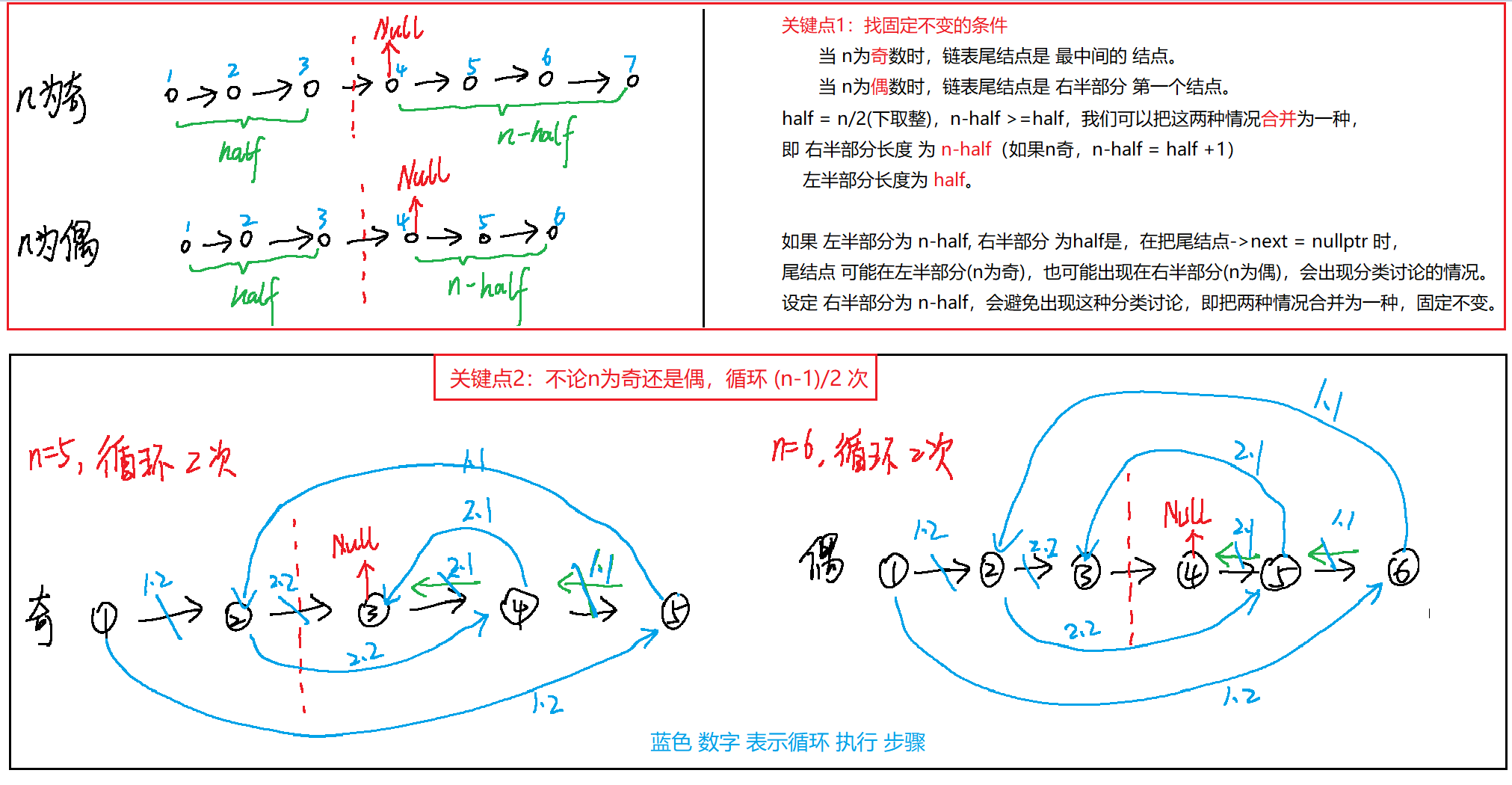# 代码

class Solution {
public:
    void reorderList(ListNode* head) {
        int n = 0;
        for (auto p = head; p; p = p->next) n++;
        if (n <= 2) return;

        int half = n / 2;
        auto a = head;
        for (int i = 0; i < half; i++) a = a->next;

        auto b = a->next;  // 此行和下一行的顺序不能换
        a->next = nullptr; // 此时a是尾结点，next赋为空
        while (b){
        // for (int i = 0; i < n - half - 1; i++){
            auto c = b->next;
            b->next = a;
            a = b, b = c;
        }

        // 注意，此处循环 (n-1)/2 次
        for (int i = 0; i < (n - 1) / 2; i++){
            b = a->next;
            a->next = head->next;
            head->next = a;
            head = a->next;
            a = b;
        }
    }
};