参考视频:

【E31 状态压缩DP 蒙德里安的梦想】 https://www.bilibili.com/video/BV1cv411b7EG/?share_source=copy_web&vd_source=859acc3f9fc77bd4a4a2953cd1bcab12

我们考虑按列摆放, 某列的各行用 0 或 1 表示摆放状态

如果某行是 1 , 表示横放, 并且向下一列伸出;
如果某行是 0 , 表示竖放, 或者由前一列横放伸出
列中各行的状态总体可用一个 01 二进制串来表示, 二进制串从左到右表示该列从上到下每一行的摆放状态

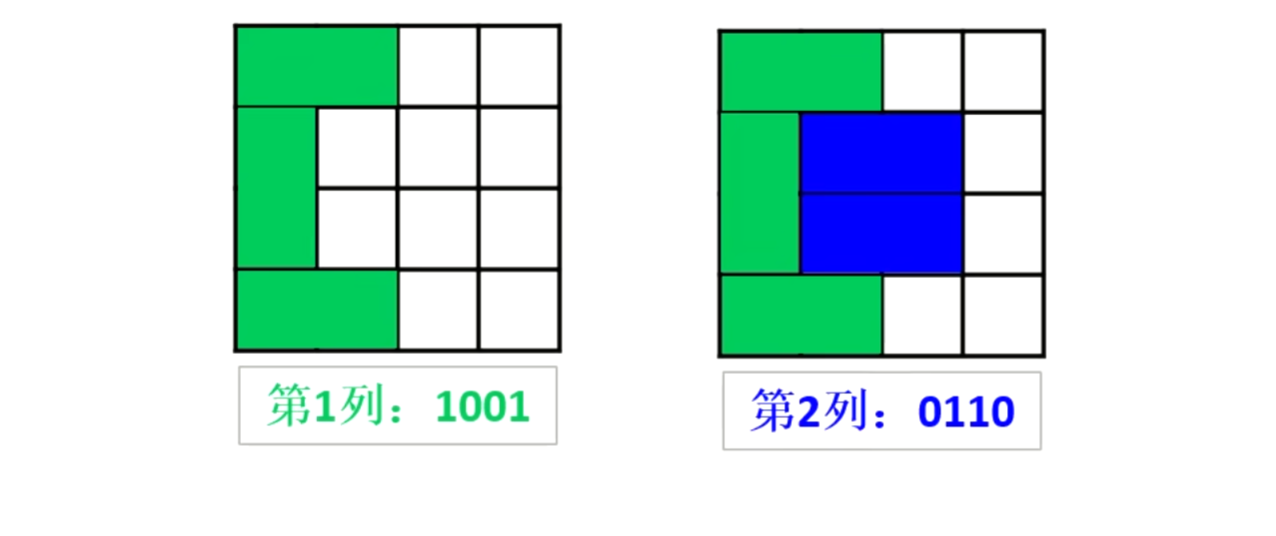
判断合法

我们定义合并列: 表示当前列与上一列的状态做或运算

如下第一个图, 第一列(参考上方定义得到1100) 1100 与 第二列(参考上方定义得到0011) 0011 做 | 运算 得到 1111, 为第二个合并列的值

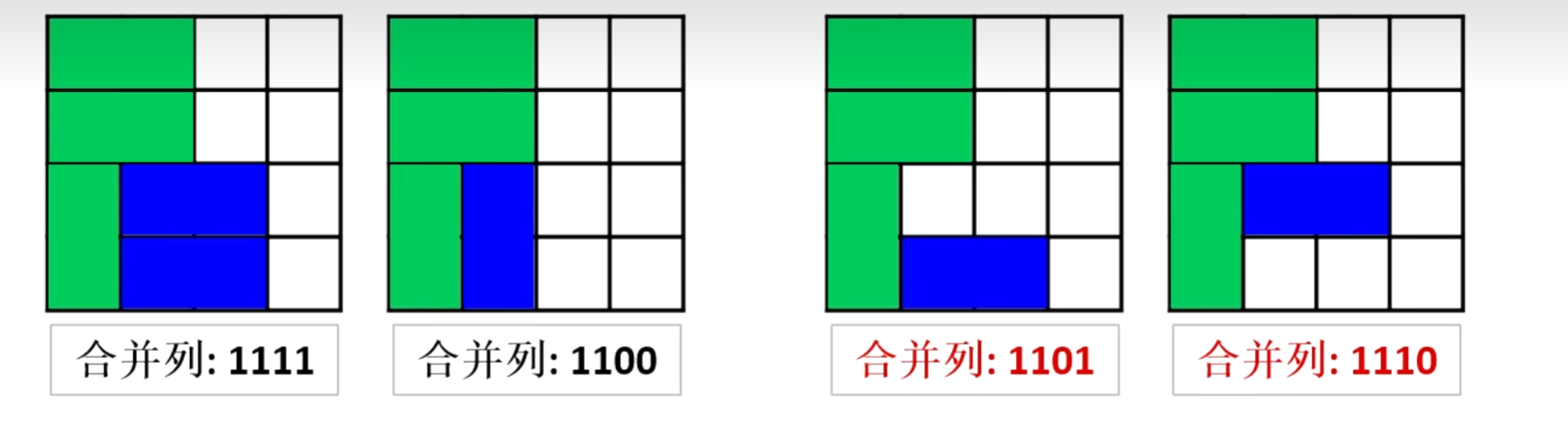
如果合并列的某行是1, 表示当前这个地方是由 当前列 或者 上一列横放伸出 而填上的

如果合并列的某行是0, 表示当前这个地方是由 上一列竖放伸出/当前列竖放填上的 或者 没有填上

如果合并列不存在连续的奇数个0, 则为合法状态 (可以结合图分析)

同时合法状态保证两列之间不能存在重叠的1

满足以上两个条件则合法

状态表示:

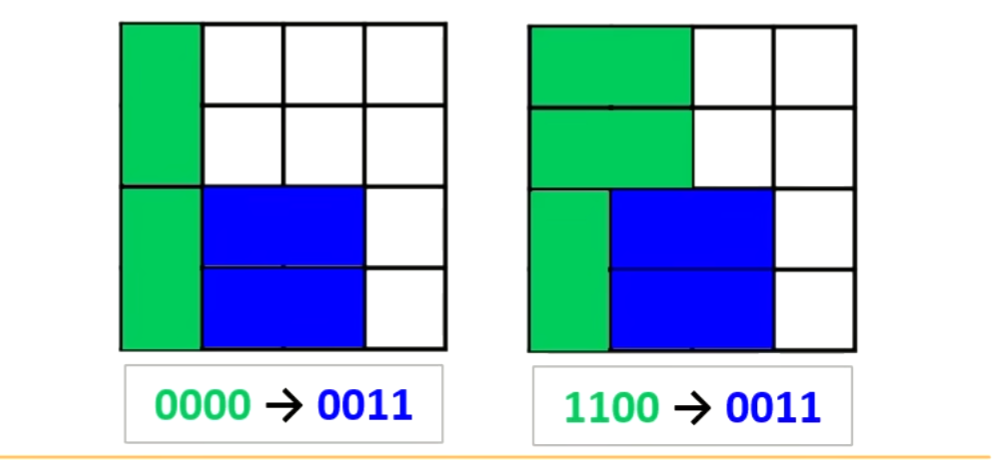
蓝色表示第二列状态, 绿色表示第一列状态, 第二列的状态需要第一列合法, 并且由第一列转移过去

$f(i, j)$ 表示摆放第 i 列, 状态为 j 时的方案数

状态计算:

$f(i-1, k) \rightarrow f(i, j)$ (其中 $k$ 一定是合法状态才行)

$f(i, j)=\sum f(i-1, k)$ (当前列的方案由之前所有的合法方案推出)

目标:

$ans=f(m, 0)$ : 摆完第 m 列, 并且m列每一行都不向下一列伸出, 表示完全合法

我们可以先预处理出所有可能的合法的状态

C++代码

预处理:

void init() {
    //预处理出所有合法的状态, 之后只需要查表看看状态是否合法即可
    //不需要每次都计算一次合法性, 降低复杂度
    for(int i=0; i<1<<n; i++) { //枚举列的每一种状态
        st[i]=true; //标记当前状态的合法程度
        int cnt=0; //记录连续0的个数
        for(int j=0; j<n; j++)  //枚举当前列的每行的状态
            if(i>>j&1) { //如果是1就判断连续0的奇偶
                if(cnt&1){
                    st[i]=false; break;
                }
            } else cnt++; //如果是0就累加

        //由于退出上方循环的时候, 最后可能累加0
        if(cnt&1) st[i]=false; //判断最开始的连续0的奇偶
    }
}

状态递推

init();
memset(f, 0, sizeof f);
f[0][0]=1; //第0列什么都不放是一种合法状态, 由这个进行递推

for(int i=1; i<=m; i++) //枚举列
    for(int j=0; j<1<<n; j++) //枚举第i列的状态
        for(int k=0; k<1<<n; k++) //枚举第j列的状态
            if((j&k)==0 && st[j|k]) //是否满足两个合法状态
                f[i][j]+=f[i-1][k]; //统计答案

cout<<f[m][0]<<'\n';