$\Huge\color{orchid}{点击此处获取更多干货}$

动态规划

区间类动态规划问题一般都和序列相关，求解时都有短区间到长区间的合并过程，算是线性序列动态规划的一种衍生。每一个长区间可以划分为若干短区间，分别对这些短区间求状态值后，附带上合并的代价将其合并后，就是长区间的状态值。一种比较简单的考虑方式就是对于长区间$[s,e]$，选定中间的某个位置$m$为合并点，然后将$[s,m]$和$[m+1,e]$上的状态值合并，附带上两段合并的代价$w(s,e)$，就是$[s,e]$的状态值了。本问题“石子合并”是最经典的区间类动态规划问题，通过上面的简单介绍，也不难得出下面的$dp$图表：

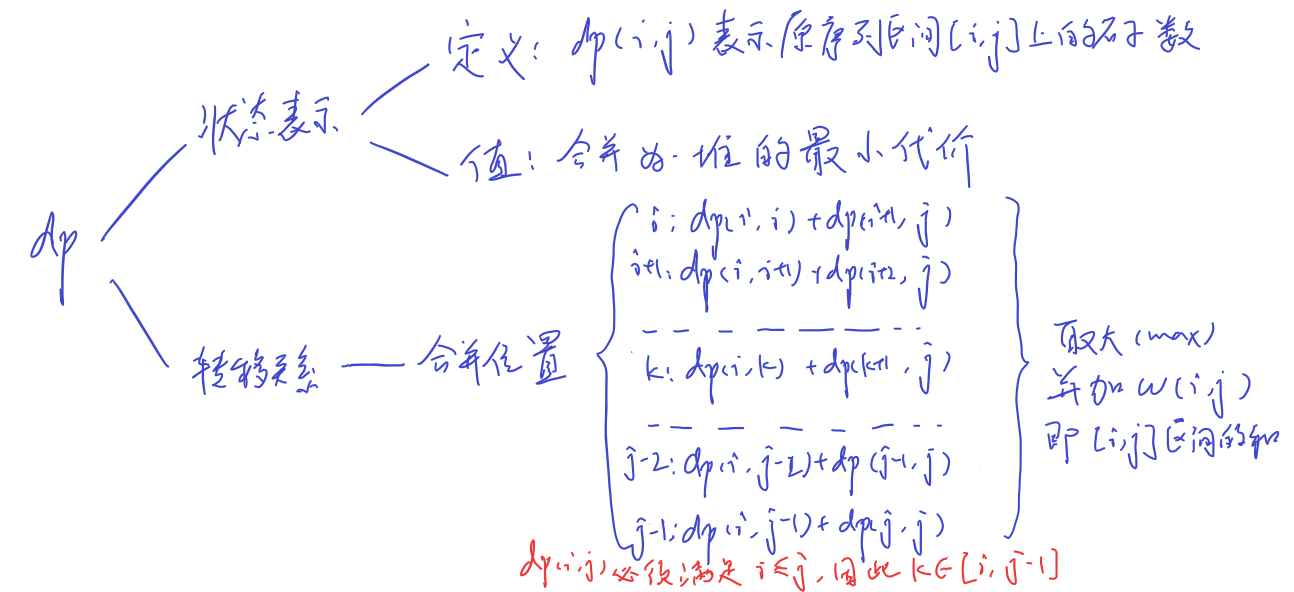
从图表上很容易就看得出，每个区间的合并位置需要挨个枚举，合并后取其大，但这是在合并后的区间已知的情况下，为了确定这个区间，我们还需要枚举区间的长度和起点位置。根据图表中的红色部分可知，当$j-1\ge i$时$k$才有意义，因此区间的长度至少需要为2，最多就是原序列的总长度。假设区间的长度为$l$，那么区间起始点的出现位置就应该是$1\sim n+1-l$之间，其中$n$是序列总长度，区间中的各个位置从1开始标号。在上述两重枚举的条件下，才能枚举合并位置，然后就是按照图表上的转移关系去递推。

C++ 代码

#include <iostream>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int* arr = new int[n + 1]();
    int** dp = new int*[n + 1];
    for (int i = 1; i <= n; i++) {
        dp[i] = new int[n + 1]();           //前述备至，构成二维数组的每条一维数组长度可以互不相同，dp[0]可以是空指针
        cin >> arr[i];
        arr[i] += arr[i - 1];               //0位置空出，既为了求前缀和，也为了对齐区间位置
    }

    for (int l = 2; l <= n; l++) {              //先枚举区间长度
        for (int s = 1; s <= n + 1 - l; s++) {  //然后枚举区间起始点
            int e = s + l - 1;
            dp[s][e] = 1e9 + 7;                 //可以在求到dp(s,e)的时候再初始化为无穷大
            for (int m = s; m < e; m++) {       //最后枚举合并位置
                dp[s][e] = min(dp[s][e], dp[s][m] + dp[m + 1][e] + arr[e] - arr[s - 1]);
            }
        }
    }
    cout << dp[1][n] << endl;
    for (int i = 1; i <= n; i++) {
        delete[] dp[i];
    }
    delete[] dp, arr;
    return 0;
}