前言,本人第一次写题解,做得不好,请多多见谅(😊)
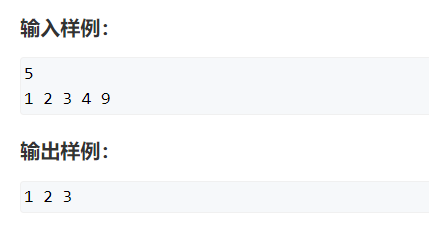
题目描述

样例
根据题目中的数据范围,n≤1e5,我们需要将时间复杂度控制在O(nlogn)以内。
题目给出了三颗宝石组合后精美程度的计算公式,这个公式相对复杂,我们需要将其进行化简,化简过程如下。注:需要知道一些最大公约数(gcd)与最小公倍数(lcm)的结论(可把a,b,c分别进行分解质因数推导得到):
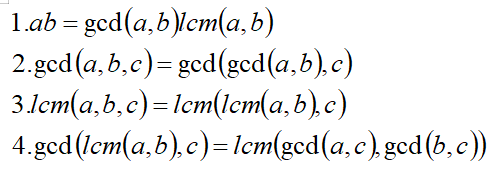

经过推导过后,我们可以将题目转化为从n个数中选3个数,使这3个数的最大公因数最大。我们当然可以通过暴力枚举这三个数,求得公因数最大值,时间复杂度O(n^3logn),不过这样似乎就没有推导公式的意义了…
我们发现Hi≤1e5,因此我们可以从这n个数中的最大的数(也可以直接从1e5)开始倒着枚举每个数,如果有一个数的倍数个数大于等于3,我们就可以输出答案,当然在这之前我们还需预处理数组中每个数的倍数。预处理的时间复杂度为O(nlogn)。代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int cnt[N]; //cnt[i]表示n个数中i出现了几次
vector<int> v[N]; //v[i]存储i的倍数
int n, m;
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i ++ ){
int x;
cin >> x;
cnt[x] ++;
m = max(m, x);
}
//预处理数组中每个数的倍数,时间复杂度为m+m/2+m/3+...+m/m=m(1+1/2+1/3+...+1/m)≈mlnm(调和级数)
for (int i = 1; i <= m; i ++ ){
for (int j = i; j <= m; j += i ){
if(cnt[j]){
for (int k = 0; k < cnt[j]; k ++ )
v[i].push_back(j);
}
}
}
for (int i = m; i >= 1; i -- ){
if(v[i].size() >= 3){
//题目要求按Hi值升序的字典序排列
sort(v[i].begin(), v[i].end());
for(int j = 0; j < 3; j ++) cout << v[i][j] << ' ';
break;
}
}
return 0;
}。