题目描述

快速幂+欧拉函数

快速幂+欧拉函数

import java.util.Scanner;

public class Main {

    static final long MOD = 998244353;

    static long qmi(long a, long b) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1)
                res = res * a % MOD;
            a = a * a % MOD;
            b >>= 1;
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        long a = scanner.nextLong();
        long b = scanner.nextLong();

        if (a == 1) {
            System.out.println(0);
            return;
        }

        long res = a, x = a;
        for (long i = 2; i <= x / i; i++) {
            if (x % i == 0) {
                while (x % i == 0)
                    x /= i;
                res = res / i * (i - 1);
            }
        }

        if (x > 1)
            res = res / x * (x - 1);

        System.out.println(res * qmi(a, b - 1) % MOD);
    }
}

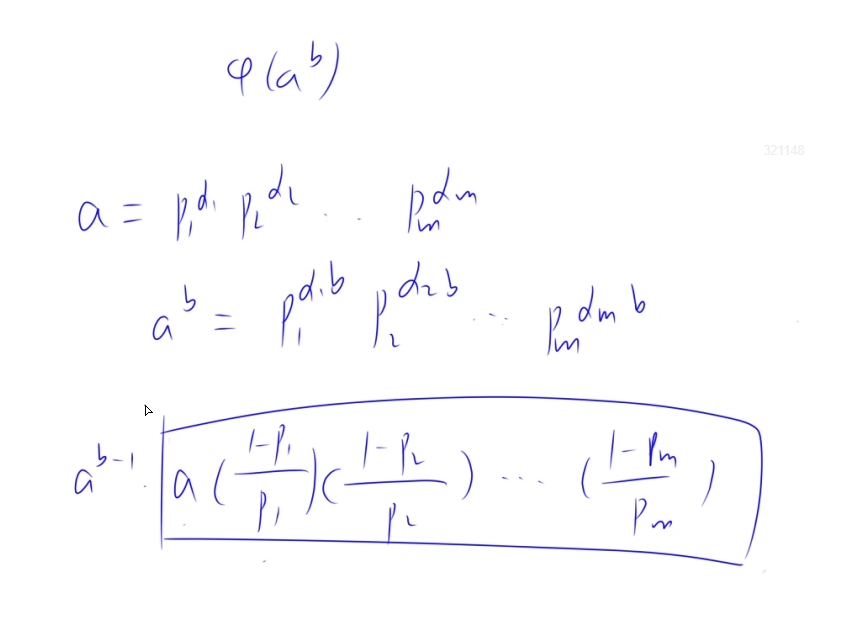
纯纯暴力

import java.util.*;
public class Main{
    static int mod =  998244353;

    public static int qmi(int a,int k){
        int res = 1;//记录答案
        //执行到k为0结束
        while (k != 0){
            //判断一下k的二进制最后一位是1还是0，如果是1执行下面的语句，说明他有这个a的2的几次方
            if((k & 1) == 1) res = (int)((long)res * a % mod);
            k >>= 1; //每一次将k的二进制向右移动一位，等待下次判断
            a = (int)((long)a * a % mod); //我们先预处理出来a的2的0至log（k）次方，然后使用这些预处理出来的数进行相乘
        }
        return  res;
    }

    //算最大的公约数  互质的话 最大公约数为1   如果b能被a整除 说明最大公约数为a
    static int gcd(int a, int b) {
        return b != 0 ? gcd(b, a % b) : a;
    }

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int a = sc.nextInt();
        int b = sc.nextInt();

        int n = qmi(a,b);

        long res = 0;

        for(int i  = 1; i < n; i++){
            if(gcd(i,n) == 1) res++;
        }

        System.out.println(res%mod);

    }
}