1、迷宫最短路

AcWing 844. 走迷宫
给定一个$n×m$的二维整数数组，用来表示一个迷宫，数组中只包含$0$ 或 $1$，其中 $0$ 表示可以走的路，$1$ 表示不可通过的墙壁。

最初，有一个人位于左上角 $(1,1)$处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 $(n,m)$ 处，至少需要移动多少次。数据保证 $(1,1)$处和 $(n,m)$处的数字为 $0$，且一定至少存在一条通路。

输入格式
第一行包含两个整数$n$和$m$。
接下来 n行，每行包含 m个整数（0 或 1），表示完整的二维数组迷宫。

输出格式
输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围
$1≤n,m≤100$

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

问题分析：
如下图所示，从起点开始，在迷宫中每走一步的过程转化为广度优先遍历中的遍历与上一层节点距离为1的节点的过程。因此，利用BFS的原理，此时我们只需要将符合要求每一层的节点(即符合要求的每一步路径走法）依次枚举出来，并且将节点是否是第一次访问到进行标记（即迷宫的该位置是否第一次走到进行标记），当我到达终点时，我们就能得出走出迷宫的最短路径时多少，并且还可以输出对应的路径。

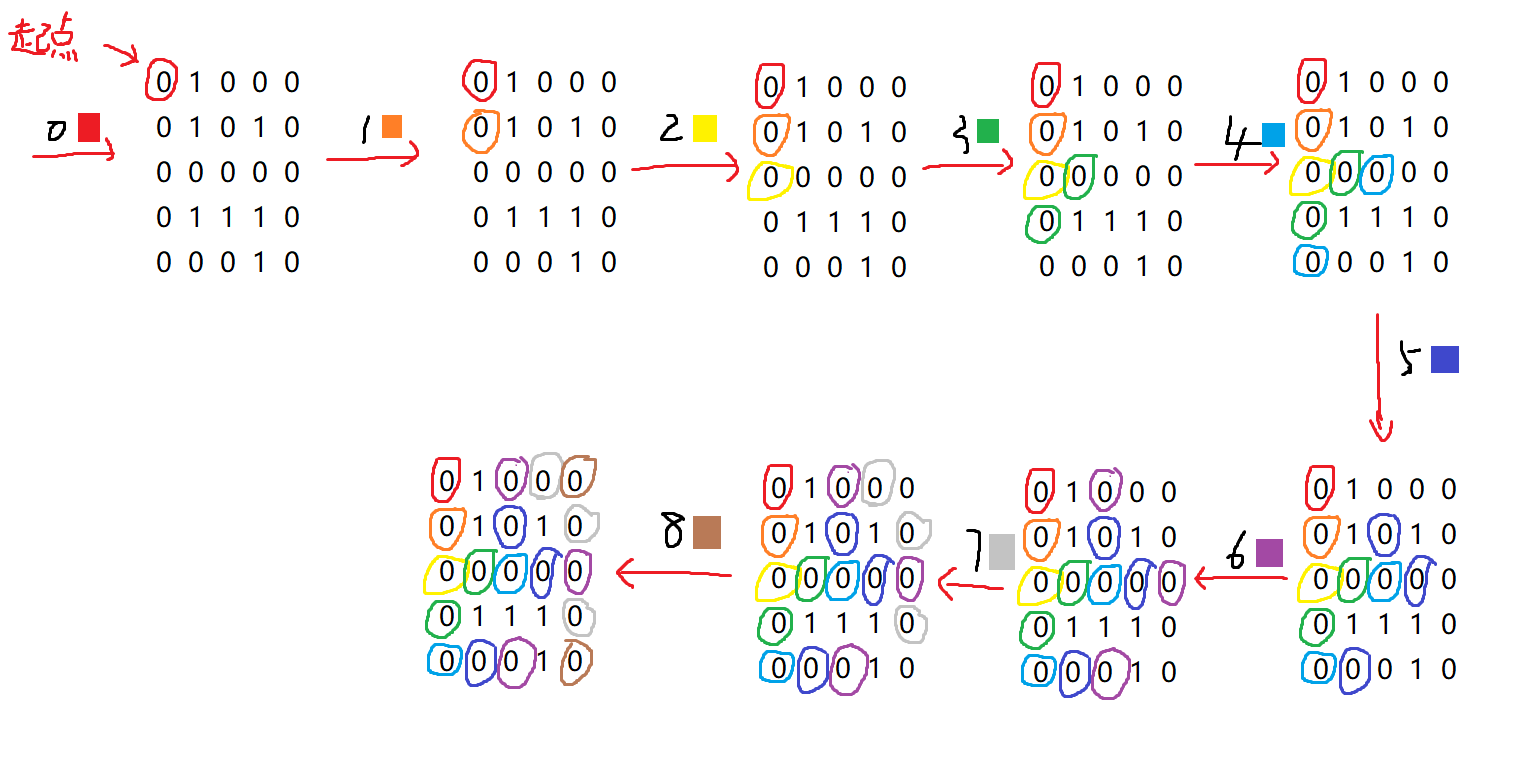
图中，描述的就是模拟样例，逐层枚举所有符合要求的的节点的过程，每一轮过程，都会新加入一层节点（即图中所示，每一轮会多一种颜色的点被圈起来，代表这一层节点被加入。如果为了更清晰可以将圈起来的所有点画成一个图进行理解）。

AC代码如下：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

const int N = 110;

int n, m;
//记录地图和某个点的最短距离
int g[N][N], d[N][N];

typedef pair<int, int >PII;

void bfs_max_path() {
    queue<PII> q;
    // 初始化所有点的最短距离为-1
    memset(d, -1, sizeof (d));
    //起点的最短距离为0
    d[0][0] = 0;
    q.push({ 0,0 });
    //x 方向的向量和 y 方向的向量组成的上、右、下、左
    int dx[4] = { -1, 0, 1, 0 }, dy[4] = { 0, 1, 0, -1 };

    while (!q.empty()) {
        //队列不空的情况
        //取队头元素
        auto t = q.front();

        q.pop();


        for (int i = 0; i < 4; i++) {
            //x,y沿着四个方向寻找路径
            int x = t.first + dx[i], y = t.second + dy[i];
            //xy在边界内，并且g[x][y]=0是空地可以走，并且之前没走过的情况
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
                //起点到当前(x,y)的最短距离，是起点到上一个点的最短距离 + 1
                d[x][y] = d[t.first][t.second]+1;
                //广搜的下一层的节点入队
                q.push({ x,y });
            }

        }

    }

    return;


}

int main() {
    cin >> n >> m;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    bfs_max_path();
    cout << d[n-1][m-1] << endl;
    return 0;

}

拓展
附带输出路径的代码如下：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
typedef pair<int, int >PII;
const int N = 110;

int n, m;
//记录地图和某个点的最短距离
int g[N][N], d[N][N];

//记录每个点最短路径的前驱节点
PII prevNode[N][N];



void bfs_max_path() {
    queue<PII> q;
    // 初始化所有点的最短距离为-1
    memset(d, -1, sizeof (d));
    //起点的最短距离为0
    d[0][0] = 0;
    q.push({ 0,0 });
    //x 方向的向量和 y 方向的向量组成的上、右、下、左
    int dx[4] = { -1, 0, 1, 0 }, dy[4] = { 0, 1, 0, -1 };

    while (!q.empty()) {
        //队列不空的情况
        //取队头元素
        auto t = q.front();

        q.pop();


        for (int i = 0; i < 4; i++) {
            //x,y沿着四个方向寻找路径
            int x = t.first + dx[i], y = t.second + dy[i];
            //xy在边界内，并且g[x][y]=0是空地可以走，并且之前没走过的情况
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
                //起点到当前(x,y)的最短距离，是起点到上一个点的最短距离 + 1
                d[x][y] = d[t.first][t.second]+1;
                //广搜的下一层的节点入队
                q.push({ x,y });
                //保存前驱节点为上一个节点
                prevNode[x][y]=t;

            }

        }

    }

    return;


}

void print_path() {
    if (d[n - 1][m - 1] == -1) {
        cout << "无法到达终点" << endl;
        return;
    }
    vector<PII> path;
    for (PII at = {n - 1, m - 1}; at != make_pair(0, 0); at = prevNode[at.first][at.second]) {
        path.push_back(at);
    }
    path.push_back({0, 0}); // 添加起点
    reverse(path.begin(), path.end()); // 反转路径，因为我们是从终点回溯到起点的
    for (auto p : path) {
        cout << '(' << p.first << ',' << p.second << ')' << "->";
    }
    cout << "终点" << endl;
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> g[i][j];
        }
    }
    bfs_max_path();
    cout << "最短路径长度: " << d[n - 1][m - 1] << endl;
    print_path();
    return 0;
}