本题运用了贪心和最短路的思想，再加上字典序的宇宙超级无敌无敌无敌的题目。

tips——字典序:
从左到右来依次观察的一种较特殊的顺序。字典序分为字母的字典序和数字的字典序。

1. 字母的字典序:
   字母的字典序中a排在第一个，z排在最后一位，大写字母与小写字母同理，排在小写字母之前。
2. 数字的字典序:
   数字的字典序其实就是我们熟知的数值排序，用sort()来解决就可以了。

接下来讲一下题目。
本题需要逆序求解01背包，我们可以把01背包看作最短路，由于背包问题的性质,需要由第n个”节点”往前推n-1个节点的可能性,每个边也都有自己的权值，分别可能是0和w[i]。用图表示是这样的。

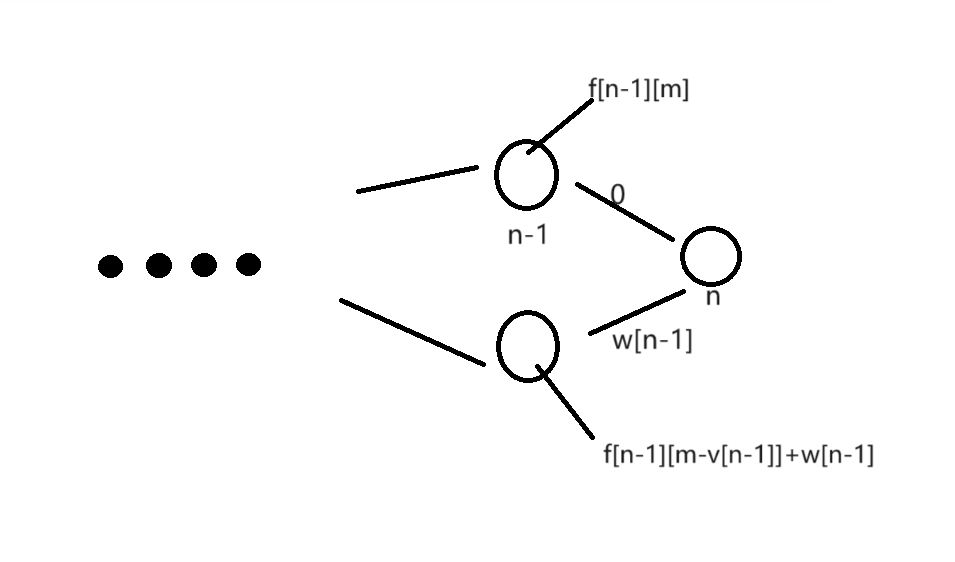
这时就引入贪心，从1~n的顺序开始选最优方案，在对待如何选择第i+1个节点时有这几种情况：
1. f[i][j]=f[i+1][j],必须选f[i+1][j]，必不选第i个物品。
2. f[i][j]=f[i+1][j-v[i]]+w[i],必须选f[i+1][j-v[i]]+w[i]，必选第i个物品
3. f[i-1][j]=f[i+1][j-v[i]]+w[i],选与不选都一样,因为要保证字典序最小，所以必选第i个物品。

欸，这时候可能就有小盆友要问了，为什么这道题要逆序求解呢，正着解它不香嘛？(啊就比如说我)
其实，这个题目有两个逆序，
一是因为这道题要求背包问题的最优方案，所要看的是一个状态是从哪一个状态转移而来的，所以要逆序遍历状态;
二是因为这道题需要按最小字典序输出最优方案，所以又要使第1个物品成为最后一个状态，又是一个逆序。

了解了这道题的思路之后，就上代码吧。

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
int f[N][N];//因为要求具体方案，所以需要用到二维数组
int v[N],w[N];//因为要求具体方案，所以也要存下每个物品的体积和价值
int n,m;

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];

    for(int i=n;i>=1;i--)//刚才讲到的第二个"逆序"
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }

    //f[1][m]是最后一个状态

    int j=m;
    for(int i=1;i<=n;i++)//刚才讲到的第一个"逆序"
    {
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])//贪心策略,注意不要漏了j>=v[i]的限定条件
        {
            cout<<i<<' ';
            j-=v[i];
        }
    }
    return 0;
}

收工！
真累呀…