单调队列法
一般实现和二进制拆分都是将多重背包问题转化为了0-1背包问题来解决,但是单调队列法不转化为0-1背包问题。那么,让我们回到最初的定义上,独属于多重背包问题的状态转移关系:
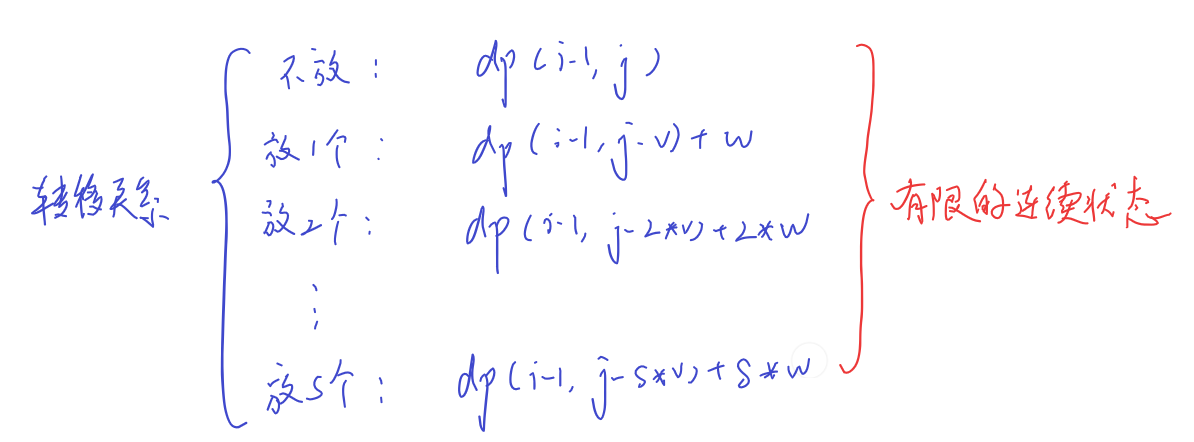
到这儿,很有可能会有人在想,能不能用完全背包问题的方式来代替表示。这里虽然在有限的状态下,不能完全替代,但是如果忽略数量限制,只要还能装下就一直往背包里装,以此来逐步限制背包的最大占用容量j,那么可以得到下面的递推式组:
(由于第i轮迭代中所有的状态都一定是从第i−1轮迭代的状态中得出的,故下面的递推式组中,dp表示第i轮,last表示第i−1轮)
{dp(j)=max{last(j),last(j−v)+w,last(j−2∗v)+2∗w,…,last(j−s∗v)+s∗w}dp(j−v)=max{last(j−v),last(j−2∗v)+w,last(j−3∗v)+2∗w,…,last(j−(s+1)∗v)+s∗w}dp(j−2∗v)=max{last(j−2∗v),last(j−3∗v)+w,…,last(j−(s+2)∗v)+s∗w......dp(r+s∗v)=max{last(r+s∗v),last(r+(s−1)∗v)+w,last(r+(s−2)∗v)+2∗w,…,last(r)+s∗w}dp(r+(s−1)∗v)=max{last(r+(s−1)∗v),last(r+(s−2)∗v)+w,…,last(r)+(s−1)∗w}......dp(r+2∗v)=max{last(r+2∗v),last(r+v)+w,last(r)+2∗w}dp(r+v)=max{last(r+v),last(r)+v}dp(r)=last(r).
其中r=j%v,相当于将当前物品最大限度装入后,背包无法利用的剩余空间。仔细对比可以发现,每一个max函数中,值最多的不会超过(s+1)个,并且它们都是相对连续的状态值,这点就跟滑动窗口最值问题很像了。下图给出了可视化描述:(分两部分,黑色表示窗口未满,红色表示窗口已满,绿色表示窗口最终状态)


将它转化为滑动窗口最大值问题之后,在第i轮迭代中,所有模v同余的j代表的状态都可以一次性求解出。因此在当前迭代中,只需要枚举所有可能的r=j%v即可。
C++ 代码
#include <iostream>
#include <deque>
#include <algorithm>
using namespace std;
deque<int> q; //单调队列,存放容量状态j
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
int* dp = new int[m + 1](),
* last = new int[m + 1]; //dp和last对应i轮和i-1轮
int v, w, s;
for (int i = 0; i < n; i++) {
cin >> v >> w >> s;
for (int r = 0; r < v; r++) { //枚举余数r
q.clear(); //每个余数对应的状态序列不一样,要清空单调队列
for (int j = r; j <= m; j += v) { //从r滑动到m,窗口长为s+1
dp[j] = last[j]; //先默认不选,然后开始选
if (!q.empty()
&& q.front() < j - s * v) { //队头的最大值滑出去了要移除
q.pop_front();
}
while (!q.empty()
&& last[q.back()] - (q.back() - r) / v * w <= last[j] - (j - r) / v * w) {
q.pop_back(); //队尾更小的值要出队
}
q.push_back(j);
if (!q.empty()) { //取队头,用队头更新当前的j(可以保证以小推大)
dp[j] = max(dp[j], last[q.front()] + (j - q.front()) / v * w);
}
//单调队列中的元素全都可以保证模v同余,因此不用担心除得浮点数
}
}
}
cout << dp[m] << endl;
delete[] dp, last;
return 0;
}
备注
单调队列法用了deque来实现,但是考虑到deque的时间常数比较大,如果主办方实在“不干人事”,连使用deque的都要恶心他们到底,那么可以利用一下其中的隐含条件,就是由于v最小是1,单调队列的大小最多也就是m+1,则可以new[]一条长度为m+1的数组q,然后参照之前“顺序队列”的实现方法,用head,tail索引指向队头队尾,然后将两索引都置于头端以代替clear,这样应该可以省不少时间(记得最后delete[]哟)

