一维差分
题目描述
输入一个长度为 n 的整数序列。接下来输入 m 个操作,每个操作包含三个整数 l,r,c,
表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
思路分析
暴力写法
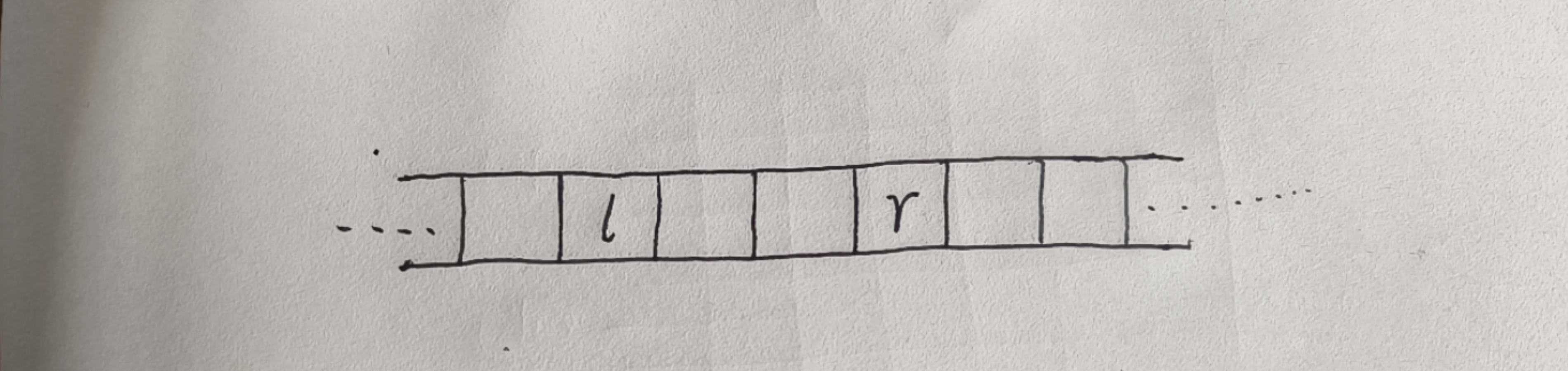
题目要求就是先给出一个整数序列,然后进行 m 次操作,每次操作都在 标号 大于等于 l 和小于等于 r 的项加上一个常数 c
我们先给 n, m 读入,然后再给 序列读入,接下来 m 次 读入一个 l 和 r 还有一个常数 c 然后 设置再设置一个循环,让每一项都加上 c
最后再输出就好了,上代码
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
int main(){
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for (int k = 1; k <= m; k ++){
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
for (int i = l; i <= r; i ++)
a[i] += c;
}
for (int i = 1; i <= n; i ++)
printf("%d ", a[i]);
return 0;
}
别急着提交,提交之后,绝对不吱声啊,时间复杂度搞一搞 数据范围 n,m都是 10 的 五次方,l 和 r 的最大差值可以达到 10 的五次方级别
然后下面两层循环相乘,10 的 10 次方,大于 10 的八次方,所以会超时,但是这里不用担心会不会爆 int 啊
每个元素最多会被操作 100000 次,每次 假设都加上最大的数 1000 ,相乘才 10 的八次方,所以不用担心爆 int
但是时间上肯定是过不去了,所以暴力不行
优化写法
怎么优化呢,先上图为敬
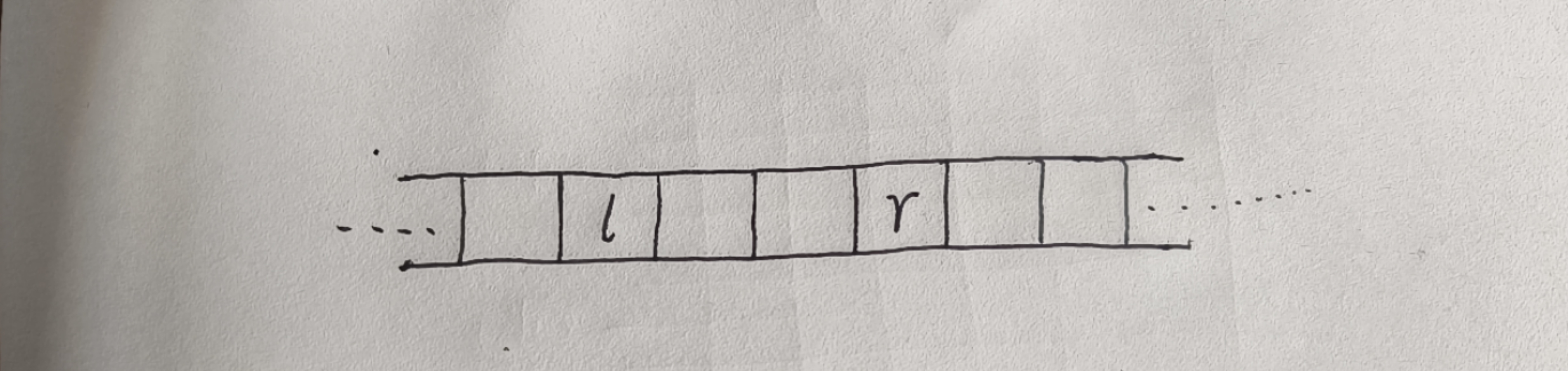
重申一下我们所要进行的核心操作,我们要做的就是在标号 大于等于 l 和 小于等于 r 的项都加上一个常数 c 对吧
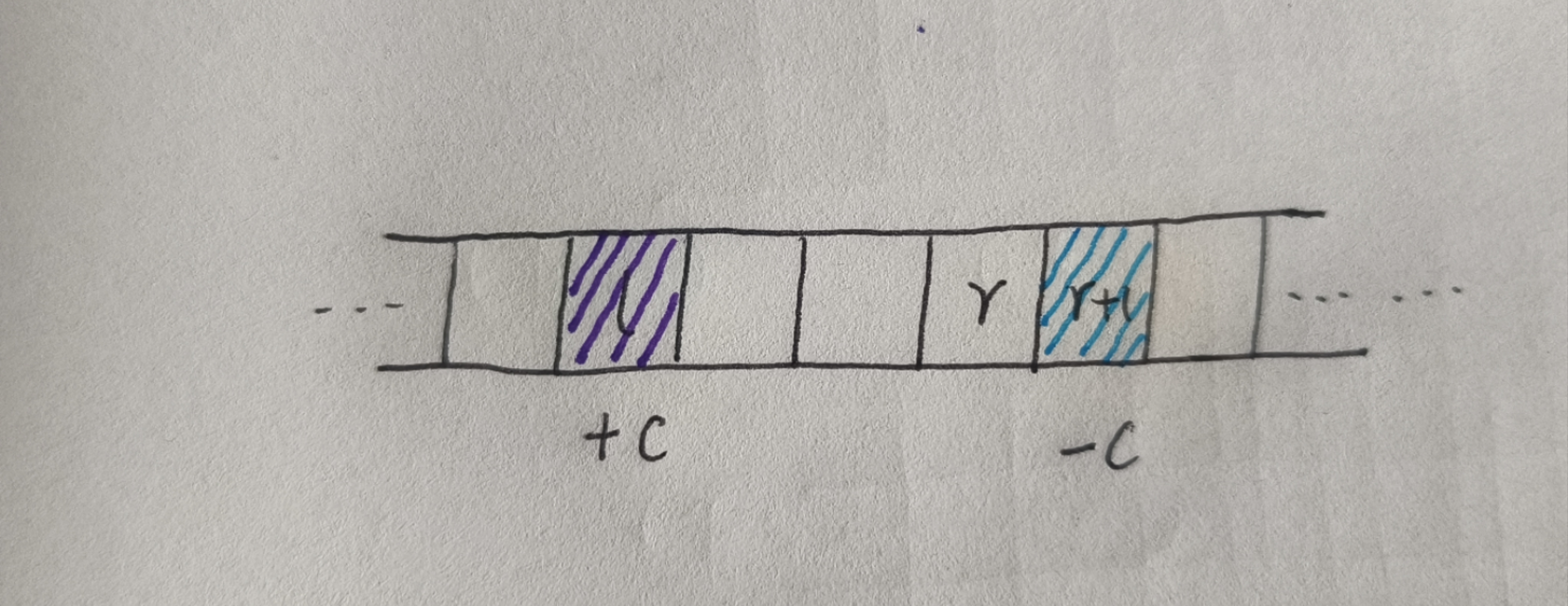
假设现在我们有一个序列,我们只是在 标号为 l 的项上 加上常数 c ,然后再在标号为 r + 1 的项上减去一个常数 c
就像是这样(注意:对这个序列的操作,不是原序列,是另开的一个序列,假设这个序列是 s,初值都是 0)
如果说我们进行一个这样的操作,s[i] = s[i] + s[i - 1] (等效于 s[i] += s[i - 1])
我们可以发现 标号小于 l 的项上的数据不会被影响,标号大于 l 的项上的数据也不会被影响,但是 标号大于等于 l 且小于等于 r 的
项上的数据都加上了一个常数 c 对于 标号大于 r + 1 的项来说,只是相当于是 加上了一个常数 c 又 减去了一个常数 c ,等于是
没有对 标号大于等于 r + 1 的项进行操作,上图
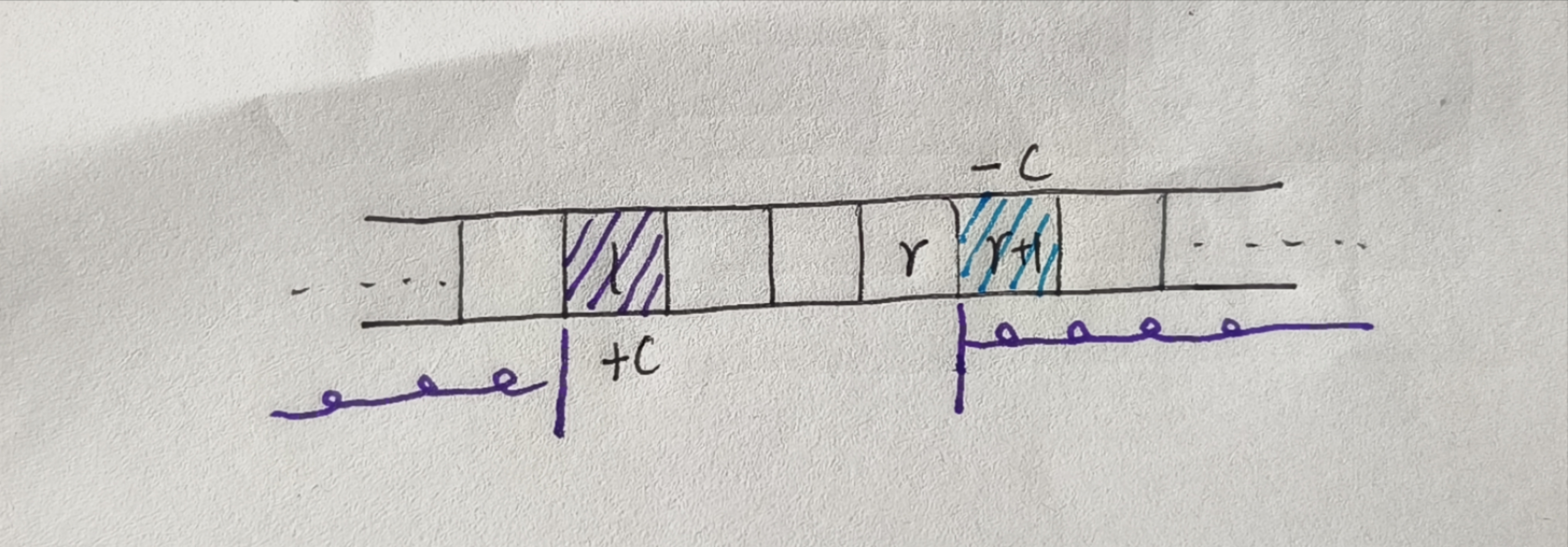
当然,这才只是处理了一次,但是处理多次也是同样的道理,现在,我们可以多次对 序列 s 进行操作,操作完成之后,再 对 s 进行
一个前 n 项和 处理,最后再依次输出 a[i] + s[i] 的结果就好了
现在的时间复杂度,主要也就是对序列进行遍历,是 O(n) 的
对于 在序列 s 上进行的操作,我们可以通过一个插入函数来实现
void insert(int l, int r, int c){
s[l] += c;
s[r + 1] -= c;
}
上代码
#include <iostream>
using namespace std;
const int N = 100010;
int a[N], s[N];
void insert(int l, int r, int c){
s[l] += c;
s[r + 1] -= c;
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for (int k = 1; k <= m; k ++){
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for (int i = 1; i <= n; i ++) s[i] += s[i - 1];
for (int i = 1; i <= n; i ++)
printf("%d ", a[i] + s[i]);
return 0;
}

