算法小结————DFS
DFS俗称暴搜,DFS可以大致分为两种题型:一种是内部搜索,另一种是外部
索。内部搜索是针对图与树内部结点的遍历(比如求解一个图或树中结点与结点
之间是否连通的问题,即连通性问题),外部搜索是针对物体状态之间的转换,
或者说是根据不同的方案而导致的物体状态的不断变化,例如本题中,每一只小
猫可以放进原来的一些组中,也可以新开辟一个组将小猫放进去,根据这些不同
的小猫放置方案,导致了分组方法上出现了变化,比如根据不同的小猫放置方案,
原本各个组的重量分别是(2,3,4),方案一中各个组的重量变成(2,5,4)、方案二
中各个组的重量变成(9,3,4)、方案三中各个组的重量变成(2,3,4,6)......
不论是外部搜索,还是内部搜索(主要是外部搜索),在写代码之前,有两
个很重要的点需要考虑:1.搜索顺序是什么 2.dfs()函数中需要哪些参数。
第一点——搜索顺序,即我们以什么样的搜索顺序去深搜,才能使我们想搜到
的所有情况都搜索到,这是dfs算法的基石,只有将搜索顺序确定下来,我们才能
进一步去思考如何去剪枝优化。
剪枝优化的方法主要有以下几种:
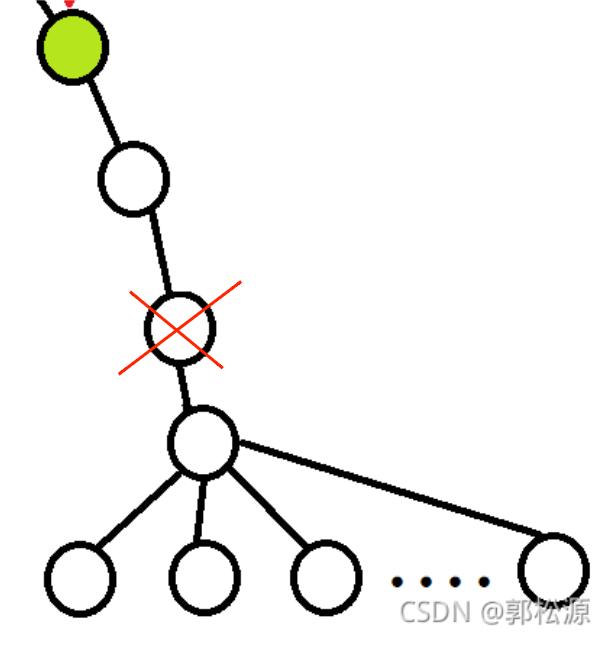
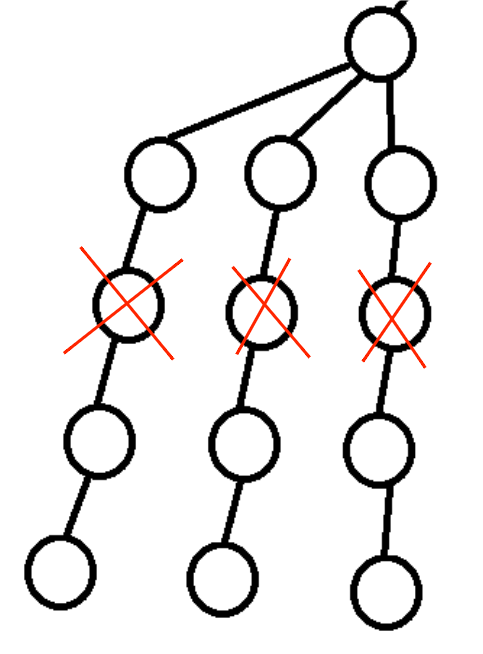
(1)优化搜索顺序——大多数情况下,优先搜索分支较少的结点。这是因为在总
结点个数确定的情况下,优先搜索决策较少的结点,如果可以剪枝,那么就能够大
大的减少搜索的数量,具体请看下图:
(2)排除等效冗余——对于不需要考虑排列顺序(先后顺序)的问题,即组
合型问题,我们要及时排除冗余情况比如对于“组合型枚举”中,像123和132就是
数字排列顺序不同,但组合相同的两种情况(具体请看——Acwing93.递归实现组合
型枚举)。
(3)可行性剪枝——将不符合题意的结点删掉,不再向下搜索
(4)最优性剪枝——将已经不再可能成为结果的结点删除,不再向下搜索。比如
题目要求找出所有方案中的最小值,我们在之前的搜索中已经找到了某完整(已
经遍历到叶子节点)的方案值为200,因此如果在其余分支中搜索时,只要中途
(还没到叶子节点)方案值已经超过200,那么就不再向下搜索
(5)记忆化搜索(DP)
本题代码
//(1)对于这一题,初步想法就是要把所有不同的小猫坐车的方法都搜索到,
// 然后判断每一种方法是否符合“每一组小猫的总重量小于W”,最后从符
// 合条件的方法中选取一个组数最少的作为最终答案。
//(2)又因为题目只要求给出最少组数值,而不需将其对应的具体分配方案记
// 录下来(并且相同组数可能会对应不同的分配方法),所以我们不需要
// 记录具体的分配方案。
//(3)为了将所有的坐车方法都搜索到,搜索顺序可以订为——每一只小猫可以
// 放在哪一辆车子里。
//(4)这一题所用到最重要的剪枝方法是:优先考虑决策少的元素,将这样的
// 元素放进搜索树中作为结点,其所用有的子树数量少
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 18;
int c[N];
bool st[N];
int sum[N];
int n, w;
int ans = 20;
void dfs(int u, int idx)
{
if(u > ans) return;
if(idx == n)
{
ans = min(ans, u);
return;
}
for(int i = 0; i <= u; i ++)
{
if(sum[i] + c[idx] <= w)
{
sum[i] += c[idx];
dfs(u, idx + 1);
sum[i] -= c[idx];
}
}
sum[u + 1] += c[idx];
dfs(u + 1, idx + 1);
sum[u + 1] -= c[idx];
}
bool compare(int a, int b)
{
return a > b;
}
int main()
{
cin >> n >> w;
for(int i = 0; i < n; i ++)
scanf("%d", &c[i]);
sort(c, c + n, compare);
//for(int i = 0; i < n; i ++)
// cout << c[i] << " ";
dfs(0, 0);
cout << ans + 1 << endl;
return 0;
}

