$\Huge\color{orchid}{点击此处获取更多干货}$

动态规划

完全背包问题的物品装入规则和0-1背包问题完全一致，但是取消了数量的限制，可以往背包中放任意数量的同种物品。状态表示虽然类似，但是转移关系就复杂多了，请看下图：

看上去还是有点难求的，毕竟只要上面递推式中的$j-k*v(i)$还不小于0，就要一直递增$k$然后频繁的求最大值，如果$j$比$v(i)$大很多的话，$max$函数就会调用特别多次。其实，这中间隐含了一个等价代换，我们尝试着在第$i$轮迭代的时候，用状态$(i,j-v(i))$来重新推导一次：

这是个意外中的收获，这样在放第$i$个物品时，长度未知的最值序列就可以全部浓缩为一个值：$dp(i,j-v(i))+w(i)$，而$dp(i,j)$就可以表示为$max\{dp(i-1,j),dp(i,j-v(i))+w(i)\}$

跟0-1背包问题一样，完全背包问题也可以用一维$dp$表来解决，但这个时候，需要正向枚举最大容量$j$，原因的话继续看上帖中的这张图：

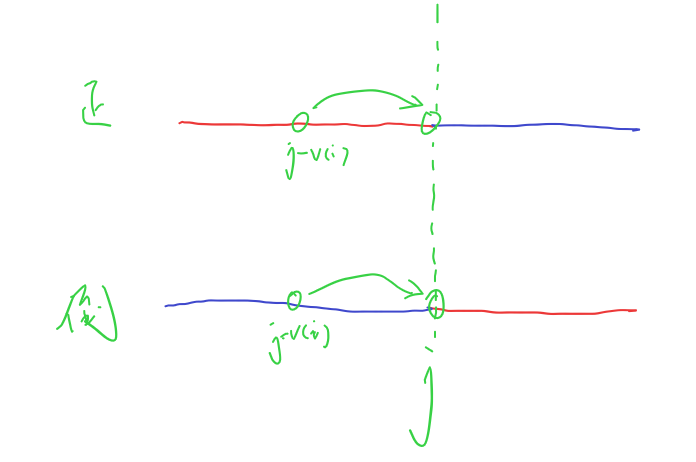
由二维$dp$表的递推式可得，第$i$轮时$dp(j)$还未更新，不选对应的是$dp(i-1,j)$，但是选的情况对应的是$dp(i,j-v(i))$，意味着大容量的$dp(j)$需要从当前迭代中已更新的小容量状态$dp(j-v(i))$来更新，用到的就是正序枚举。这个时候就要去判断$j-v(i)$是不是能一直保持着不大于0了。

C++ 代码

#include <iostream>
#include <algorithm>
using namespace std;

struct obj {
    int v, w;
    Obj() {}
    Obj(int _v, int _w) : v(_v), w(_w) {}
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    Obj* objs = new Obj[n + 1];
    for (int i = 1; i <= n; i++) {
        cin >> objs[i].v >> objs[i].w;
    }
    int* dp = new int[m + 1];
    for (int i = 1; i <= n; i++) {  
        for (int j = 0; j <= m; j++) {  //除了正序枚举和负值判断，其余和0-1背包完全一致
            if (j - v[i] < 0) {
                continue;
            }
            dp[j] = max(dp[j], dp[j-objs[i].v] + objs[i].w);
        }
    }
    cout << dp[m] << endl;
    delete[] dp;
    delete[] objs;
    return 0;
}