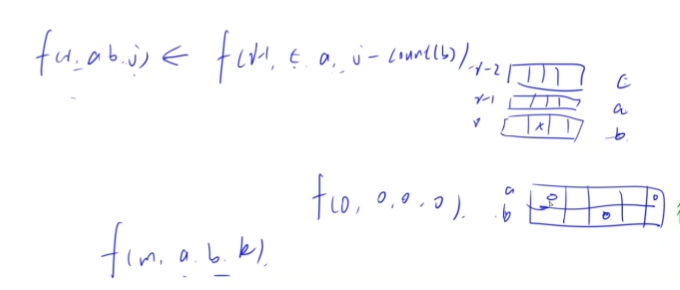题目描述

dfs(回溯)会TLE

dfs(回溯)

import java.util.*;

public class Main {
    static final int N = 110;
    static final int MOD = 1000000007;
    static int[][] cnt = new int[N][N];
    static int res = 0;
    static int[] dx = {-2, -1, 1, 2, 2, 1, -1, -2};
    static int[] dy = {1, 2, 2, 1, -1, -2, -2, -1};
    static int n, m, k;

    static void dfs(int x, int y, int sum) {
        if (sum == k) {
            res = (res + 1) % MOD;
            return;
        }
        if (y > m) {
            y = 1;
            x++;
            if (x > n) return;
        }

        dfs(x, y + 1, sum); //(x,y)不放马

        if (cnt[x][y] == 0) {//如果(x,y)可以放马，就放马
            // 更新一下状态(在(x,y)处放马后，哪些位置不能放马了)
            cnt[x][y]++;
            for (int i = 0; i < 8; i++) {
                int a = x + dx[i], b = y + dy[i];
                if (a < 1 || a > n || b < 1 || b > m) continue;
                cnt[a][b]++;
            }

            dfs(x, y + 1, sum + 1); //放马后，马的数量sum要 +1

            // 恢复现场
            cnt[x][y]--;
            for (int i = 0; i < 8; i++) {
                int a = x + dx[i], b = y + dy[i];
                if (a < 1 || a > n || b < 1 || b > m) continue;
                cnt[a][b]--;
            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        k = scanner.nextInt();
        dfs(1, 1, 0); // 从（1，1）这个位置开始放马，最开始总共放了0个马
        System.out.println(res);
        scanner.close();
    }
}

状态压缩DP

import java.util.*;

public class Main {

    static final int N = 110, M = 1 << 6, K = 21, MOD = (int) (1e9 + 7);
    static int[][][][] f = new int[N][M][M][K];

    //求二进制里面一的个数
    static int get_count(int x) {
        int res = 0;
        while (x != 0) {
            res++;
            x -= x & -x;
        }
        return res;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int k = scanner.nextInt();

        //初始的时候就一种方案 就什么都不放 也就是互相攻击不了
        f[0][0][0][0] = 1;

        for (int i = 1; i <= m; i++) {
            for (int a = 0; a < 1 << n; a++) {
                for (int b = 0; b < 1 << n; b++) {
                    //判断a和b会不会攻击到   a向左移两位或b向左移两位
                    if ((b & (a << 2)) != 0 || (a & (b << 2)) != 0) continue;
                    for (int c = 0; c < 1 << n; c++) {
                        //判断a和c不会攻击到 a向左移两位或c向左移两位
                        if ((c & (a << 2)) != 0 || (a & (c << 2)) != 0) continue;
                        //判断b和c不会攻击到 a向左移1位或b向左移1位
                        if ((c & (b << 1)) != 0 || (b & (c << 1)) != 0) continue;
                        int t = get_count(b);
                        for (int j = t; j <= k; j++) {
                            f[i][a][b][j] = (f[i][a][b][j] + f[i - 1][c][a][j - t]) % MOD;
                        }
                    }
                }
            }
        }

        int res = 0;
        for (int a = 0; a < 1 << n; a++) {
            for (int b = 0; b < 1 << n; b++) {
                res = (res + f[m][a][b][k]) % MOD;
            }
        }
        System.out.println(res);
    }

}