过河卒

题目描述

如图，在 A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。
同时在棋盘上的任一点有一个对方的马 （如上图的C点），该马所在的点和所有跳跃一步可达的
点成为对方马的控制点。
例如图中 C 点上的马可以控制 9 个点 （图中的 P1，P2…P8 和 C）。
卒不能通过对方马的控制点。

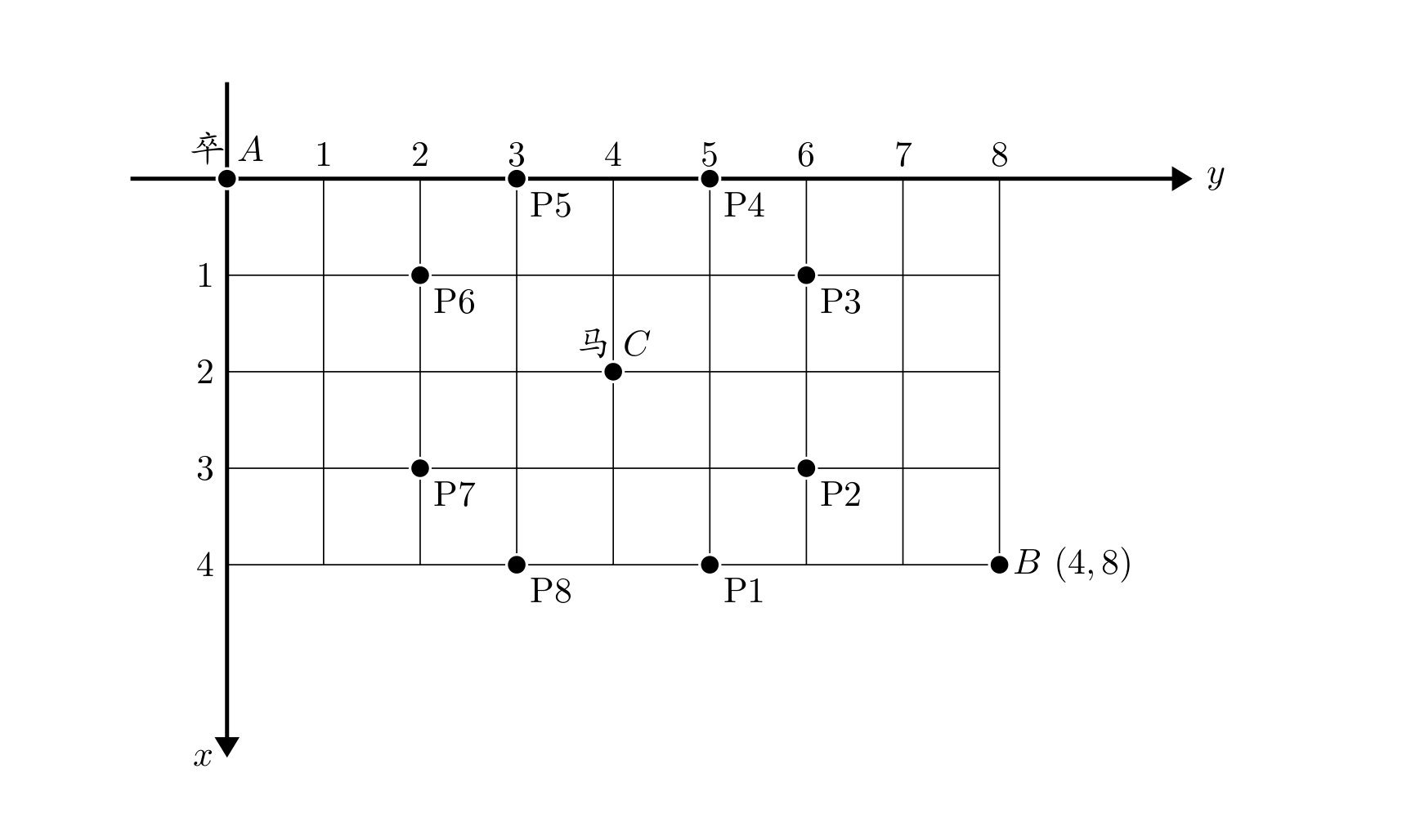
棋盘用坐标表示，A 点的坐标为 (0,0)、B 点的坐标为 (n,m)，马的位置 C 点的坐标为 (X,Y)
（约定: C≠A，同时 C≠B）。
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。

输入格式

共一行，包含 n,m,X,Y。

输出格式

一个整数，表示路径条数。

数据范围

1≤n,m≤20, 0≤X≤n, 0≤Y≤m

输入样例

6 6 3 2

输出样例

17

大体思路 —— 朴素版本

（1）初始化一张地图

可以开一个 bool 类型的二维数组，名为 map，用作地图，读入马的所在位置的坐标，然后给每个坐标的值都 加一，
根据 “马走日” ，可以先初始化一个向量数组 dx[] 和 dy[] ，根据马坐在位置的横纵坐标分别加上相对应的向量数组的值，
对 卒 所不能到达的点的坐标进行确定，当然要确定坐标是否合法

（2）路径数量的计算

开一个二维数组 path[][]，path[i][j] 的数值表示从 起始点（左上角）到 （i，j）这个点的可以行得通的路径的数量

由于卒一次只能走一步，假如说现在 卒 要走到 A 点，那么走到 A 点的路径的数量，就等于 从 B 点走到 A 点的路径数量加上
从 C 点走到 A 点的路径的数量之和，如果说 B 点是马的控制点，那么走到 A 点的路径的数量就只等于从 C 点走到 A 点的路径数量
同理，如果 C 点是马的控制点，那么走到 A 点的路径的数量就只等于从 B 点走到 A 点的路径数量，如果 B，C 都是马的控制点，
那么走到可以走到 A 点的路径数量就是 0，当然，我们可以给 path[][] 开成全局变量形式的数组，那么，无论 A 点 B 点的状态如何
path[i][j] 的计算方程都是 path[i][j] = path[i][j - 1] + path[i - 1][j]，但是需要注意的，是给 A 点进行判断，判断其是否为
马的控制点，如果是的话，就不做处理，就是 0，很明显，我们的状态计算很像是前缀和，所以我们认定 （1，1）是起始点
但是图中很明显，起始点是 （0，0）对吧，所以我们为了给这个 “图” 向右下平移一个单位，需要给每个我们读入的值 加一

上代码

#include <iostream>

using namespace std;

const int N = 30;

typedef long long LL;
/*
我们可以假设没有马的存在，从左上角到右下角这条对角线上的点的数值，（path 的值）
成指数级别增长，会爆 int 的，所以给 path 数组开城 long long 类型
*/

bool map[N][N];
LL path[N][N];

int dx[] = {0, -2, -2, -1, -1,  1,  1,  2,  2};
int dy[] = {0, -1,  1, -2,  2, -2,  2, -1,  1};

int main(){
    int n, m, x, y;
    scanf("%d%d%d%d", &n, &m, &x, &y);
    n ++, m ++, x ++, y ++;

    map[x][y] = true;
    for (int i = 1; i <= 8; i ++){
        int a = x + dx[i], b = y + dy[i];
        if (a >= 1 && a <= n && b >= 1 && b <= m)
            map[a][b] = true;
    }

    path[1][0] = 1;
    /*
        下面相当于是一个 dp 的过程，是从 （1，1）这个点开始的，但是不能直接初始化 path[1][1] = 1，
        不然一开始path[1][1] 的数值就被覆盖掉了，应该初始化上方与其相邻的点，或者左方与其相邻的点
        也就是说，这里写 path[0][1] = 1，其实也可以。直接 path[1][1] = 1的写法也行，但是需要多个判断
        我觉得代码不好看，写在下方作为参考吧
    */
    for (int i = 1; i <= n; i ++){
        for (int j = 1; j <= m; j ++){
            if (!map[i][j])
                path[i][j] = path[i - 1][j] + path[i][j - 1];
        }
    }
    /*
    path[1][1] = 1; // 直接初始化 path[1][1] = 1 的写法
    for (int i = 1; i <= n; i ++){
        for (int j = 1; j <= m; j ++){
            if (!map[i][j] && !(i == 1 && j == 1))
                path[i][j] = path[i - 1][j] + path[i][j - 1];
        }
    }
    */

    printf("%lld\n", path[n][m]);

    return 0;
}

你以为就这么结束了吗？ NO！

有没有一种可能，就是这个马的位置比较变态，直接给人 卒 壁咚了，有可能的对吧，还有就是有些马控制点右下方的某些点，
根本就没必要遍历对吧，但是朴素写法中，我们直接特判 + 两重循环，也是可以过的对吧，我们可以优化一下，用数组模拟一个队列
只存储有必要遍历的点，没必要遍历的点，我们直接就不考虑

对此我们还要在初始化一个关于 卒 走向的变量数组 ddx[] 和 ddy[]，接下来的写法就类似于bfs 或者 dfs 了（没分太清），
后期的实践过程当中发现运行效率并不如朴素写法高，在此就不进行过多赘述了
但是还是有值得一提的地方的，这个代码是最开始我想到的写法，测试一下，样例可以通过，但是提交，
就会报错，说是越界，然后我给队列的长度都开到极限了，还是说是越界，一开始觉着，每个点最多不过是进出队列两次
明明已经开的很大了，还是会越界
去找了老师，尝试输出了一下 tt 的数值，发现到最后，tt 的数值是超过 2 * n * m 的，最后发现，进出队列的次数
不是那么简单，其实是呈指数级别增长的，非常恐怖，老师的建议就是另开一个bool 类型的数组 st[][]，来判断这个点
是否已经进入过 队列 了，如果进入过，就不再重复进入了，然后这个写法的代码终于是通过了
下面是这个代码，留作 广搜 或者 深搜 写法的参考吧

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 100, M = 500;

typedef pair<int, int> PII;
typedef long long LL;

bool map[N][N];
LL path[N][N];
bool st[N][N];
PII q[M];

int dx[] = {0, -2, -2, -1, -1,  1,  1,  2,  2};
int dy[] = {0, -1,  1, -2,  2, -2,  2, -1,  1};
int ddx[] = {0, 1, 0}, ddy[] = {0, 0, 1};

int main(){
    int n, m, x, y;
    scanf("%d%d%d%d", &n, &m, &x, &y);
    n ++, m ++, x ++, y ++;

    map[x][y] = true;
    for (int i = 1; i <= 8; i ++){
        int a = x + dx[i], b = y + dy[i];
        if (a >= 1 && a <= n && b >= 1 && b <= m)
            map[a][b] = true;
    }

    q[0] = {1, 1};
    path[1][1] = 1;
    int hh = 0, tt = 0;
    while (hh <= tt){
        auto t = q[hh ++];
        for (int i = 1; i <= 2; i ++){
            int a = t.first + ddx[i], b = t.second + ddy[i];
            if (a >= 1 && a <= n && b >= 1 && b <= m && !map[a][b]){
                path[a][b] = path[a - 1][b] + path[a][b - 1];
                if (!st[a][b])
                q[ ++ tt] = {a, b}, st[a][b] = true;
                //cout << tt << ' ';
            }
        }
    }

    printf("%lld\n", path[n][m]);

    return 0;
}

如果对你的学习有所帮助，那就大方的给俺点个赞吧~~~