动态规划
背包问题的通用形式化描述就是在背包容量一定的情况下,将某些给定的物品(具备一定的容量和价值)放入背包,使得背包内总价值最大化。根据放入物品的数量特征,可以分为四类:
1. 分数背包问题,每种物品只有一件,当背包剩余容量不够物品整体放入时,可以选取物品的一部分放入。这个可以用贪心算法解决,在此不予讨论
2. 0-1背包问题,每种物品只有一件,这些物品要么不放进背包,要么就将整体放进背包(0-1由此得名),剩余容量不够时不能取物品的一部分放入。
3. 完全背包问题,每种物品有无数件,一件物品放入背包的规则与0-1背包问题相同。
4. 多重背包问题,每种物品的数量有限(会事先给定),物品放入的规则还是和0-1背包问题相同。
这次重点是0-1背包问题,由于没有了线性序列的辅助,状态表示和转移关系变得更抽象。为了方便分析,我们将所有物品看成一个“序列”,然后给出下面的图表:

(上面写错了,j的含义是最大占用的容量,而不是剩余容量)
在状态转移的过程中,我们需要挨个考虑每个物品,对于第i个物品,如果不选它,那么总容量不变,在前面的i−1个物品中选择,最多占用背包的j容量时,背包中物品的最大价值dp(i−1,j)和dp(i,j)应该是保持相等的;如果最大容量比第i个物品的体积大,且装入第i个物品时,前面i−1个物品对应的最大容量不包含当前物品的体积v[i],对应的状态值应该是dp(i−1,j−v[i]),在此基础上,再累加当前物品的价值w[i]
由上面的递推式可得,dp(i,x)的状态永远只能从dp(i−1,x)的状态推出,因此我们可以把dp表的第一维省略掉。并且,对于“容量”来说,在放入物品的时候,一直都是从小容量状态去推出大容量状态,而只有j−v[i]≥0时才能放物品。因此,这里我们可以从背包的总容量开始向v[i]倒序枚举,保证大容量的状态总是由小容量的状态推出。
至于为什么是“倒序枚举”,这地方是一个重点,后面还会涉及到,需要先说清楚。在dp(i,x)状态下,一维dp表里的所有元素都相当于dp(i−1,x),需要在之后的迭代中将dp(i,x)状态的各个值覆盖上去,下面的图中,用红色表示已经覆盖的dp(i,x)状态值,蓝色表示未覆盖的dp(i−1,x)值,则正序和倒序枚举时,会出现以下的状况:
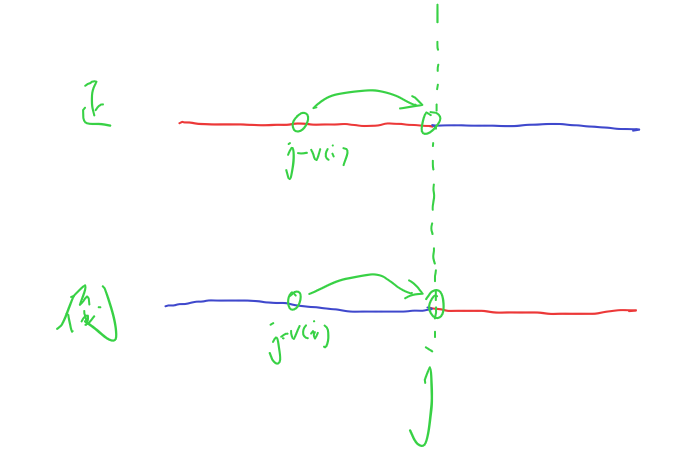
dp(i,j)要用dp(i−1,j−v(i))得出,但是正序枚举的情况下,dp(i,j)用了dp(i,j−v(i))得出,是不对的,所以要用倒序枚举的方式。当然对于追求稳健,想用可解释性更强的二维dp表来解决的,那么无论按照正序还是倒序去枚举容量都是可行的,因为在二维表下,dp(i,x)是独立于dp(i−1,x)的
C++ 代码
下面代码中主要演示一维表法,二维表法放在注释里
#include <iostream>
#include <algorithm>
using namespace std;
struct obj {
int v, w;
Obj() {}
Obj(int _v, int _w) : v(_v), w(_w) {}
};
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
Obj* objs = new Obj[n + 1];
for (int i = 1; i <= n; i++) {
cin >> objs[i].v >> objs[i].w;
}
int* dp = new int[m + 1]; //一维dp表,用来代表容量
for (int i = 1; i <= n; i++) { //在前i个物品中选
for (int j = m; j >= objs[i].v; j--) { //剩余容量为j
dp[j] = max(dp[j], dp[j-objs[i].v] + objs[i].w);//递推
}
}
/*
* 二维表法:
* for (int i = 1; i <= n; i++) {
* for (int j = 0; j <= m; j++) {
* dp[i][j] = dp[i - 1][j];
* if (j - objs[i].v >= 0) {
* dp[i][j] = max(dp[i][j], dp[i-1][j-objs[i].v]+objs[i].w);
* }
* }
* }
* cout << dp[n][m] << endl;
*/
cout << dp[m] << endl; //输出dp[m]即剩余容量为背包总容量
delete[] dp;
delete[] objs;
return 0;
}

