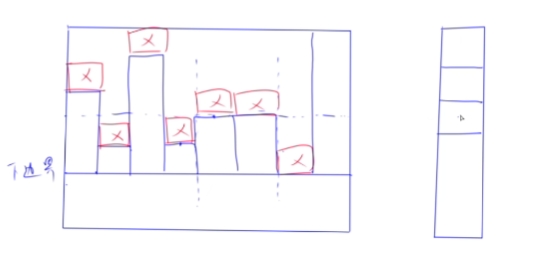
题目描述

二维前缀和和单调栈

利用单调栈可以看：
AcWing 131 直方图中最大的矩形: https://www.acwing.com/solution/content/236523/

二维前缀和(暴力求解)

import java.util.*;

public class Main {
    static final int N = 3010;
    static int[][] g = new int[N][N];
    static int[][] s = new int[N][N];

    static void init(int x , int y){
        for(int i = 1; i <= x; i++)
          for(int j = 1; j <= y;j++)
             s[i][j] = g[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

    }

    private static int sumPrefix(int x1, int y1, int x2, int y2) {
        return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
    } 

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int P = scanner.nextInt();


        for (int i = 0; i < P; i++) {
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            g[x][y] = 1;
        }

        init(n,m);

        int res = 0;
        for (int l = 1; l <= n; l++)
          for(int r = l; r <= n; r++)
            for (int up = 1, down = 1; down <= m; down ++) {
                    while (up <= down && sumPrefix(l, up, r, down) != 0)
                        up ++;
                    res = Math.max(res, (down - up + 1) * (r - l + 1));
                }

        System.out.println(res);
    }
}

单调栈

import java.util.*;

public class Main {
    static final int N = 3010;

    public static int work(int[] h, int m) {
        int[] l = new int[N];
        int[] r = new int[N];
        int[] stk = new int[N];
        int top = 0;

        h[0] = h[m + 1] = -1;
        top = 0;
        stk[0] = 0;
        for (int i = 1; i <= m; i++) {
            while (h[stk[top]] >= h[i]) top--;
            l[i] = stk[top];
            stk[++top] = i;
        }

        top = 0;
        stk[0] = m + 1;
        for (int i = m; i > 0; i--) {
            while (h[stk[top]] >= h[i]) top--;
            r[i] = stk[top];
            stk[++top] = i;
        }

        int res = 0;
        for (int i = 1; i <= m; i++)
            res = Math.max(res, h[i] * (r[i] - l[i] - 1));
        return res;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int P = scanner.nextInt();
        int[][] g = new int[N][N];
        int[][] h = new int[N][N];

        for (int i = 0; i < P; i++) {
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            g[x][y] = 1;
        }

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                //如果格子没被破坏
                if (g[i][j] == 0)
                    //当前往上数的没有被破坏的格子数量 = 上一个格子往上数的没有被破坏的格子数量 + 1
                    h[i][j] = h[i - 1][j] + 1;

        int res = 0;
        for (int i = 1; i <= n; i++)
            res = Math.max(res, work(h[i], m));

        System.out.println(res);
    }
}