题目描述
给定N件物品以及一个体积为V的背包,每件物品可以用无限次,第 i 件物品的体积是 v[i],
价值是w[i],求解将哪些物品装进背包,可以使这些物品的总体积不大于背包的体积,且总价值最大。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。接下来
有N 行,每行两个整数v[i],w[i],用空格隔开,分别表示第i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<v[i],w[i]≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
问题分析
1.状态表示
定义一个二维数组f[M][M],M = 1010
集合
f[i][j] 表示从前 i件物品中选,且总体积不大于j的选法的集合
属性
f[i][j] 的数值代表其所对应集合中的选法的最大价值的数值
2.状态计算 —— 朴素版本
如果现在计算到 f[i][j], 我们可以分成两种情况,即 选 与 不选 第 i 件物品,
如果不选,那好办,直接 f[i][j] = f[i - 1][j]
如果选,那么首先还是要给第 i 件物品腾出来地方,那么
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]) 注:此处 f[i][j] = f[i - 1][j];
但是与 01背包问题不同的事是,01背包问题每个物品最多只能用一次,但是完全背包,每个
物品可以用多次,只要不超过背包的体积就行,我们可以假设每个物品用 k 次,先展示一波核心代码
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j]; // 可调整
for (int k = 1; k * v[i] <= j; k ++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * v[i]);
}
}
但是很明显啊,上面标注的那一行代码可以调整,只需要给 k 的起始值变一下就好了(古娜拉黑暗之神)
变成下面这个样子
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
for (int k = 0; k * v[i] <= j; k ++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
如果说我们第 i 件物品用k 次,相当于是我们前 i - 1 件物品当中选,且总体积不大于 j - k * v[i],
然后再将从前 i - 1 件物品当中选,且总体积不大于 j - k * v[i] 的选法的集合的最大价值的数值
加上 k * w[i],最后再与当前状态比较,取较大值即可
2.状态计算 —— 一次优化
上面的代码是三层循环,最坏时间复杂度是 O(nmm),数据范围是 1000,所以最坏时间复杂度是 10 的
9次方,大于 10 的8次方,可以说是百分百会超时了,如何来优化呢,我们可以看一下状态计算方程
f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w, f[i-1][j-2v[i]]+2w[i], f[i-1][j-3v[i]]+3w[i], …);
我们要做的是就是从 max 括号中的一堆数据里面选出最大值,假如说现在这个 j 是大于等于 v[i]的,那么,
我们可以在往前看几步,就是 f[i][j - v[i]] 的计算过程,
f[i][j-v[i]] = max(f[i-1][j-v[i]], f[i-1][j-2v[i]]+w[i], f[i-1][j-3v[i]]+2*w[i],…);
现在我们将这两个状态计算方程做一下对比,如下
f[i][j-2*v[i]] = max( f[i-1][j-2*v[i]] , f[i-1][j-3*v[i]]+1*w[i], ...);
f[i][j-v[i]] = max( f[i-1][j-v[i]], f[i-1][j-2*v[i]]+ w[i], f[i-1][j-3*v[i]]+2*w[i], ...);
f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i], f[i-1][j-2*v[i]]+2*w[i], f[i-1][j-3*v[i]]+3*w[i], ...);
对比一下,我么不难发现,下一层数据(后面的数据)与上一层数据(前面的数据),对齐后有些只是差了w[i],而且这些数据计算过程前面的部分是相同的,我们可以给朴素版本的代码做一下进一步的优化,如下
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
现在最坏时间复杂度是 O(n*m),最坏是 10 的六次方,低于10 的八次方,已经可以通过了
2.状态计算 —— 二次优化
这次优化主要是对空间上面的优化,将数组从二维降到一维,我们直接去掉一个维度
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[j] = f[j]; // 恒等式,删除
if (j >= v[i]) // 改变二层循环的条件
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
最终是这个样子
for (int i = 1; i <= n; i ++){
for (int j = v[i]; j <= m; j ++){
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
是不是有种似曾相识的感觉,没错,就是 01背包问题代码终极写法的前一步(01背包优化解释图)
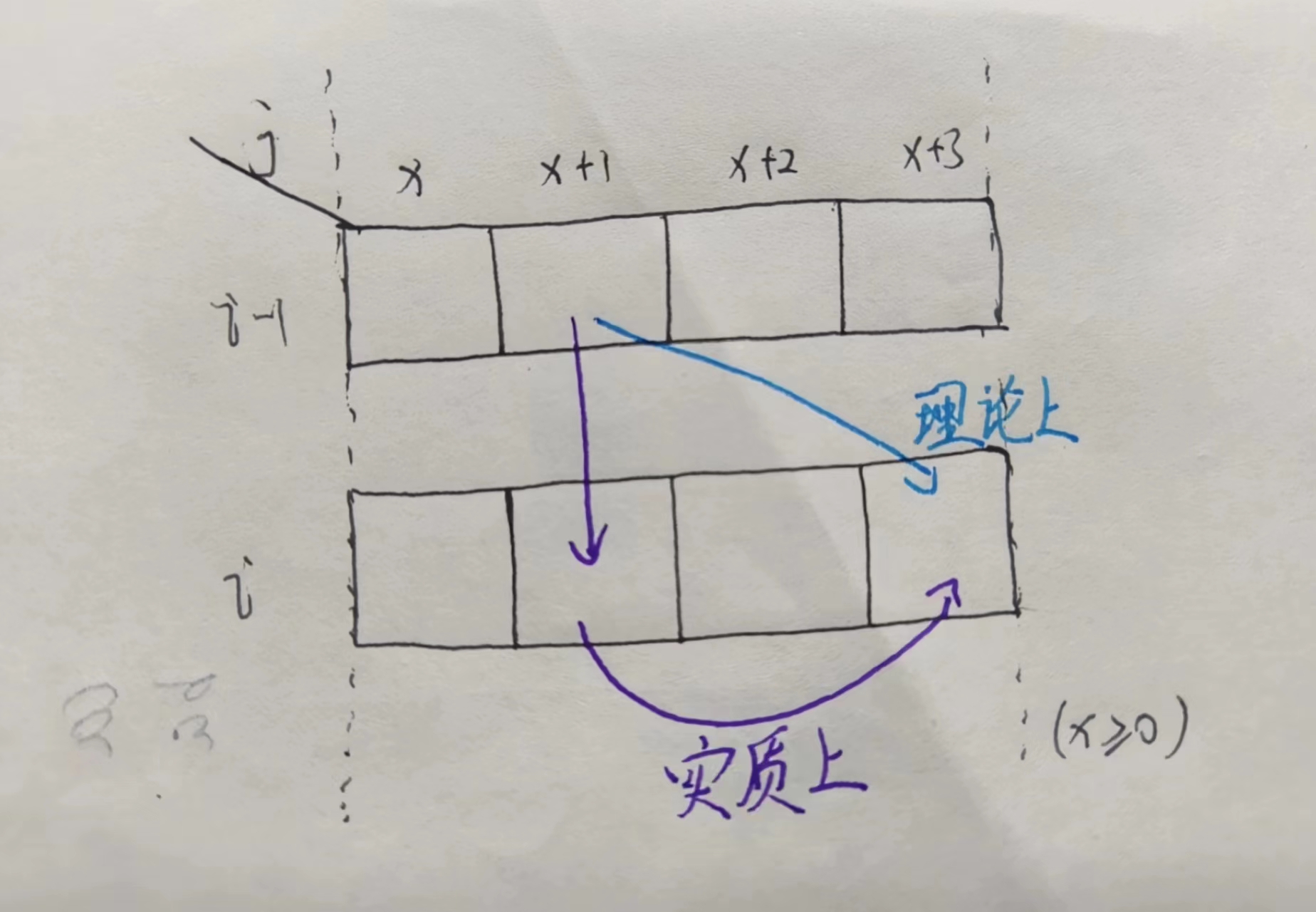
对于 01背包问题,我们的状态计算可以说是要严格依赖于上一层数据,而且必须是前一层数据
对于 完全背包问题,我们基本上依赖的是本层数据,对于 01背包问题,我们需要将二层循环进行倒序,
倒序完成之后,才是终极写法,而完全背包问题,则不需要进行倒序,现在的写法就是终极写法
上代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];
int ff[N];
int main(){
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
/*
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
for (int k = 0; k * v[i] <= j; k ++){
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
*/
/*
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
*/
for (int i = 1; i <= n; i ++)
for (int j = v[i]; j <= m; j ++)
ff[j] = max(ff[j], ff[j - v[i]] + w[i]);
printf("%d\n", ff[m]);
return 0;
}

