$\Huge\color{orchid}{点击此处获取更多干货}$

最优子结构与重叠子问题

在介绍动态规划问题之前，需要先介绍一些很重要的前置知识：最优子结构与重叠子问题
首先是“最优子结构”性质，它的含义为：总问题的最优解可以通过子问题的最优解得到。这里面暗含了分治思想，将一个大问题分解成若干个相同的小问题，对这些小问题分别求最优解，可以从中推导出大问题的最优解。下面看一个例子：

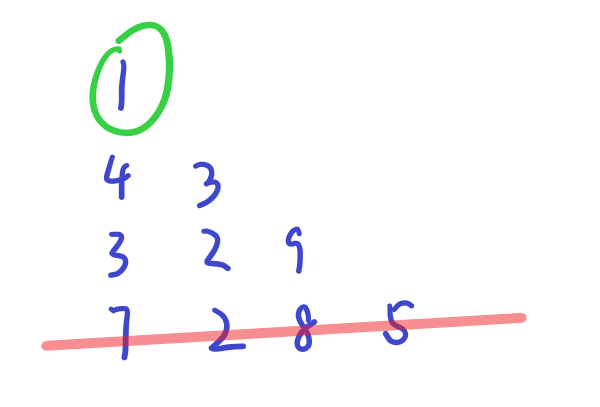
上图中是一个“数字三角形”，需要从三角形顶部（绿色位置）开始走，每次只能朝着下一层，向正下方或右下方走一步，走到红线上任意一个位置时停止，将路径上所有的数加起来，求得累加和的最大值。假设我们将行、列号从1开始标，用$t(i,j)$表示第$i$行$j$列的数，用$dp(i,j)$表示从顶部走到第$i$行$j$列，那么可以得出下面的递推式：$dp(i,j)=t(i,j)+max\{dp(i-1,j),dp(i-1,j-1)\}$。这里我们默认当$i$或者$j$为0时，$dp(i,j)=-\infty$。这个递推式的由来是：既然只能朝着正下方和右下方走一步，那么$dp(i,j)$对于每一对$(i,j)$来说都只能从正上方和左上方推导出来，这样就把问题分解为了求从顶部走到某位置“正上方”和“左上方”时路径上的最大值这两个子问题，然后从他们俩的最大值中可以导出总问题的最优解。

接下来介绍“重叠子问题”性质，它的含义是：不同的问题推导序列可能会到达相同的状态。还是上面的数字三角形，当位于某个$(i+1,j+1)$时，它可以使用子问题$(i,j)$的值，然而位于$(i,j+1)$时它也可以使用$(i,j)$的值。这个$(i,j)$就属于“重叠”的子问题，为了避免计算两次，需要将这个状态对应的值保存在一张表中，这张表就是上面的$dp$表。构造此表时迭代法和递归法都可以使用，下面的演示代码中将使用递推法。

C++ 代码

#include <iostream>
#include <climits>
#include <algorithm>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    int** triangle = new int*[n + 1], 
        ** dp = new int*[n + 1];
    for (int i = 0; i <= n; i++) {
        triangle[i] = new int[n + 1];
        for (int j = 1; j <= i; j++) {                      //输入数字三角形
            cin >> triangle[i][j]
        }
        dp[i] = new int[n + 1];
        fill(dp[i], dp[i] + n + 1, INT_MIN);                //dp表所有初值都为负无穷
    }
    dp[1][1] = triangle[1][1];
    for (int i = 2; i <= n; i++) {
        for(int j = 1; j <= i; j++) {                       //按递推式构造dp表
            dp[i][j] = triangle[i][j] + max(dp[i - 1][j - 1], dp[i - 1][j]);
        }
    }
    cout << *max_element(dp[n] + 1, dp[n] + n + 1) << endl; //最优解（最大值）在第n行中产生
    return 0;
}