二分

题目分析

    本题不论是用二分的方法，还是使用双指针的方法，最重要的一步就是对c[n]数组进行
从大到小排序，并用画数轴的方式直观的体现题目信息。
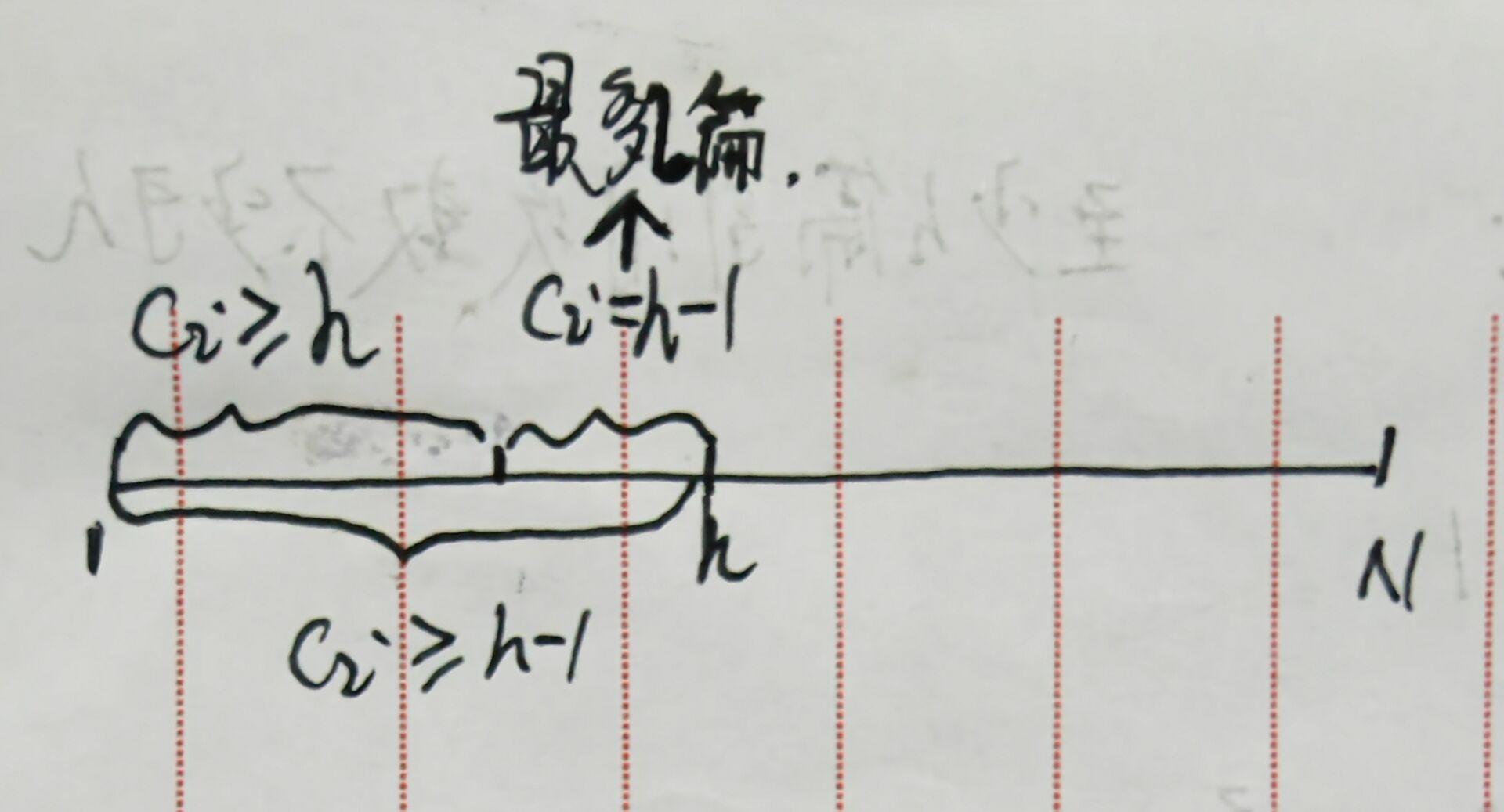
    对于要求解的答案h，其含义是c[n]数组中至少会有h个数的值大于等于h且h取到最大。
我们发现h的取值范围是[0, n](n是论文的数量)，并且当取了(h,n]区间内的数作为h的话，
一定在c[n]中找不到h个不小于h的数；当取了[0,h]区间内的数作为h的话，一定能找到h个
不小于h的数。因此可见h的取值具有两段性，因此我们可以用二分的方法去二分答案——h。
    由于我们已经对c[n]进行了从大到小的排序，我们只需利用每次二分的结果——mid，去
判断c[mid]是否大于等于h，若是则说明mid在区间[0, h]中，若不是则说明mid在区间(h,n]
中。又因为我们可以给 l个数加 1，所以我们可以判断c[mid]是否大于等于(h - 1)，并且
c[mid-l]是否大于等于h。

代码展示

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int c[N];
int n, L;
int b_search(int l, int r)
{
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(c[mid] >= mid - 1 && (mid - L <= 0 || c[mid - L] >= mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}
bool compare(int a, int b)
{
    return a > b;
}
int main()
{
    cin >> n >> L;
    for(int i = 1; i <= n; i ++)
        scanf("%d", &c[i]);
    sort(c + 1, c + n + 1, compare);
    int l = 0, r = n;
    int h = b_search(l, r);
    cout << h << endl;
    return 0;
}

双指针

题目分析

    如果对于寻找结果h，我们不通过二分的方法去查找，而是通过从0到n去遍历的话，那
么对于每一轮遍历i，都要满足（1）c[i] >= i-1 （2）1 ~ i中等于(i - 1)的最多有l个，
    若（1）成立，则可进行（2）的判断：
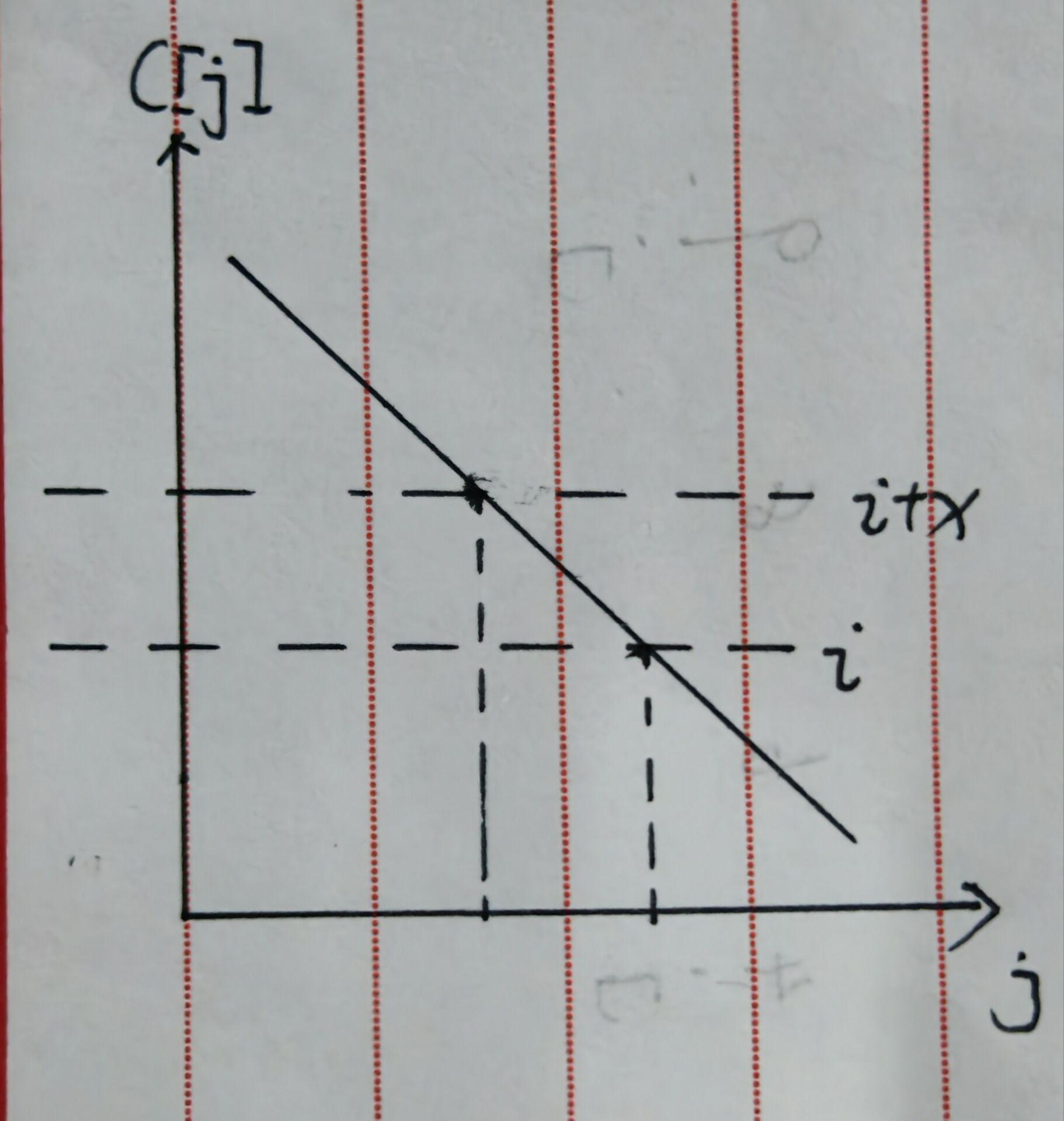
    我们可以在数组c[n]中找到最后一个大于等于i的元素下标j，然后再用(i - j)和l进行
比较，若i - j <= l的话，则说明i符合h的性质。在每一轮遍历中，我们都要去寻找j，如果
不进行任何优化，则时间复杂度时O(n^2)的，但是我们发现随着i的增大，j的值会减小（因
为数组c[n]是从大到小排序的）因此两个指针之间是有单调关系的，可以使用双指针算法用
O(n)的时间寻找到每个i对应的j。
    其实吧，对于每一轮遍历i，我们也可以用“二分”中的——（1）c[i]是否大于等于(h-1)
（2）c[i-l]是否大于等于h来判断；同样，“二分”中也可以用该方法中i - j 是否小于等于l
去判断。

代码展示

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;
int c[N];
int n, l;
bool compare(int a, int b)
{
    return a > b;
}
int main()
{
    cin >> n >> l;
    for(int i = 1; i <= n; i ++)
        scanf("%d", &c[i]);
    sort(c + 1, c + n + 1, compare);
    int h = 0;
    for(int i = 1, j = n; i <= n; i ++)
    {
        if(c[i] >= i - 1)
        {
            while(c[j] < i && j >= 1) j --;
            if(i - j <= l) h = i;
        }
        else break;
    }
    cout << h << endl;
    return 0;
}