题目描述
给定N件物品以及一个体积为V的背包,每件物品只能用一次,第 i 件物品的体
积是 v[i], 价值是w[i],求解将哪些物品装进背包,可以使这些物品的总体积不大于背包的体积,且总价值最大。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。接下来
有N 行,每行两个整数v[i],w[i],用空格隔开,分别表示第i件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<v[i],w[i]≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
问题分析
1.状态表示
定义一个二维数组f[M][M],M = 1010
集合
f[i][j] 表示从前 i件物品中选,且总体积不大于j的选法的集合
属性
f[i][j] 的数值代表其所对应集合中的选法的最大价值的数值
2.状态计算——二维版本
(1) 第 i 件物品不选
当计算到 f[i][j] 时,如果第i件物品不选,那么f[i][j] 的值等于只从前i - 1件物品中选,
并且总体积不大于 j 的选法的集合所对应的最大价值,即 f[i][j] = f[i - 1][j]
(2) 第 i 件物品选
当计算到 f[i][j] 时,如果说选择第 i 件物品,那么首先得考虑是否能装下第 i 件物品,
即得比较一下 j 与 v[i]的大小,如果 j < v[i],那么是装不下的
f[i][j] 的计算仍然是 f[i][j] = f[i - 1][j]
如果 j >= v[i],那么表示可以装下那么 f[i - 1][j], f[i - 1][j - v[i]] + w[i] 两者
之间的最大值就是 f[i][j]的值,即 f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
此处对 f[i - 1][j - v[i]] + w[i], 做一些解释,就是当我们要选第 i 件物品
时(装的下的情况下),我们首先要腾出一部分空间 v[i] 给第 i 件物品,相当于是我们
从前 i - 1 件物品当中选,并且总体积不大于 j - v[i] 的选法的集合的最大价值加上
第 i 件物品的价值 w[i]
那么这一部分的核心代码就是这样了,如下
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
}
}
整体二维版本代码如下
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];
int main(){
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
}
}
printf("%d\n", f[n][m]);
return 0;
}
状态计算——一维优化
从上上面的分析不难看出,第 i 层数据的计算依赖于第 i - 1 层的数据,模拟一下这个计算
过程,更直观的感受一下第 i 层数据的计算对第 i - 1 层数据的依赖性
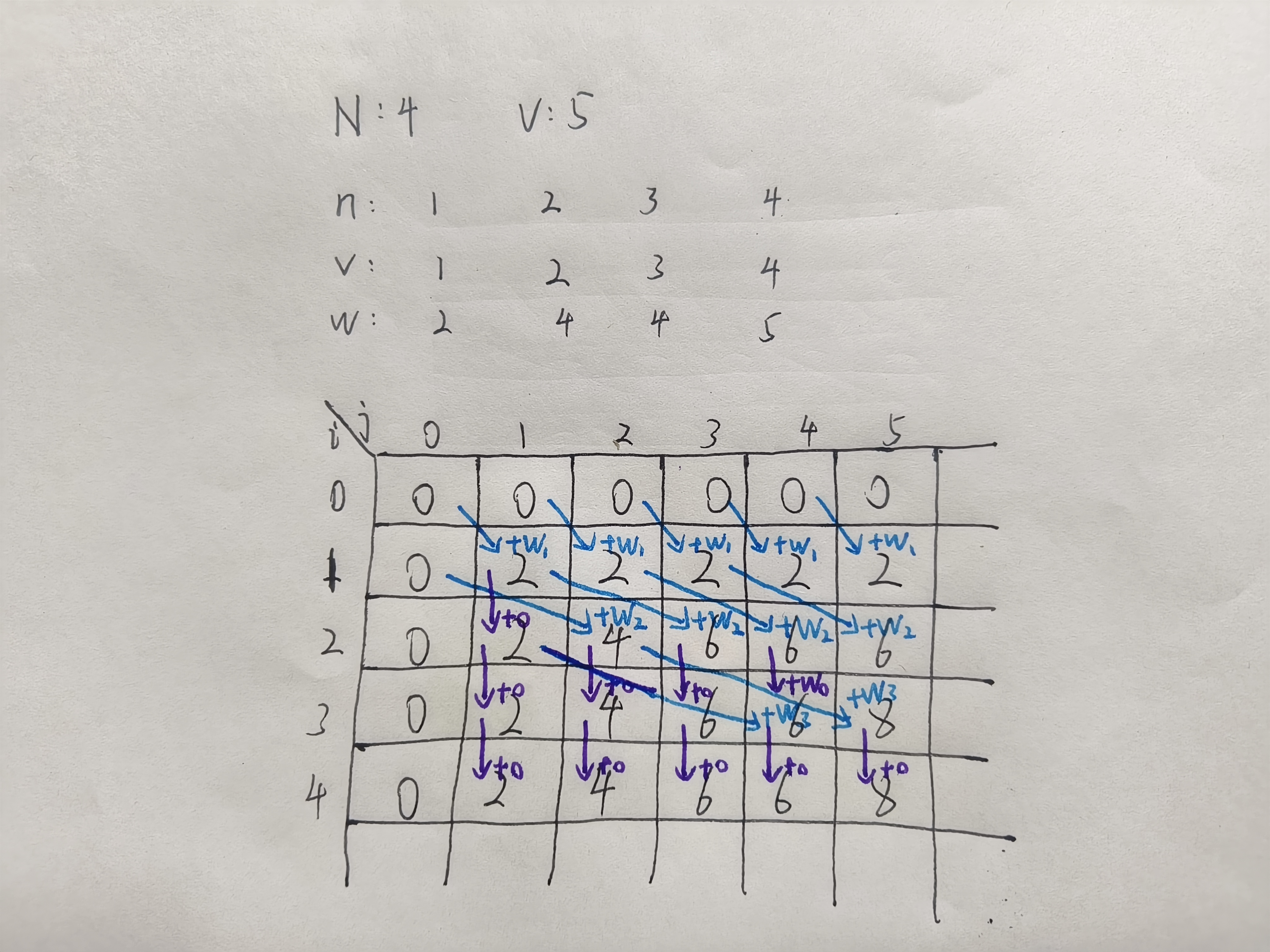
首相我们可以给 f[N][N] 去掉一个维度了,巴啦啦能量,小魔仙变身 f[N][N] –> f[N]
然后(注意下方代码的注释)
for (int i = 1; i <= n; i ++){
for (int j = 0; j <= m; j ++){
f[i][j] = f[i - 1][j];
/*
f[i][j] = f[i - 1][j] 去掉第一个维度 --> f[j] = f[j] 恒等式,直接删除
就好了,对于下方的这个判断,我们直接去掉,然后让第二层循环从 j = v[i]
开始,然后下方的二维再变成一维
*/
if (j >= v[i])
f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
}
}
现在展示一下变身(巴啦啦能量)成功后的代码
for (int i = 1; i <= n; i ++){
for (int j = v[i]; j <= m; j ++){
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
你以为这就结束了吗,no no no,还没有,因为我们计算只用到了两层数据,但是一开始我们
有很多层数据,我们要对其进行一个空间上的优化对吧
我们还发现本层数据的计算依赖于上一层数据,我们先是对f[N][N}进行了降维,还有就是变动了
一些计算方程,但是就上面这个代码的计算逻辑,是与题目要求不相符的
我们还是先想象一个二维数组,但是只有两层,来解释为什么就 “变质”了
需要注意的事是,f[N] 是一维的,所以虽然我们想象成两层,其实只有一层哈,不要被误导了
对此,我们将这个两层分开画
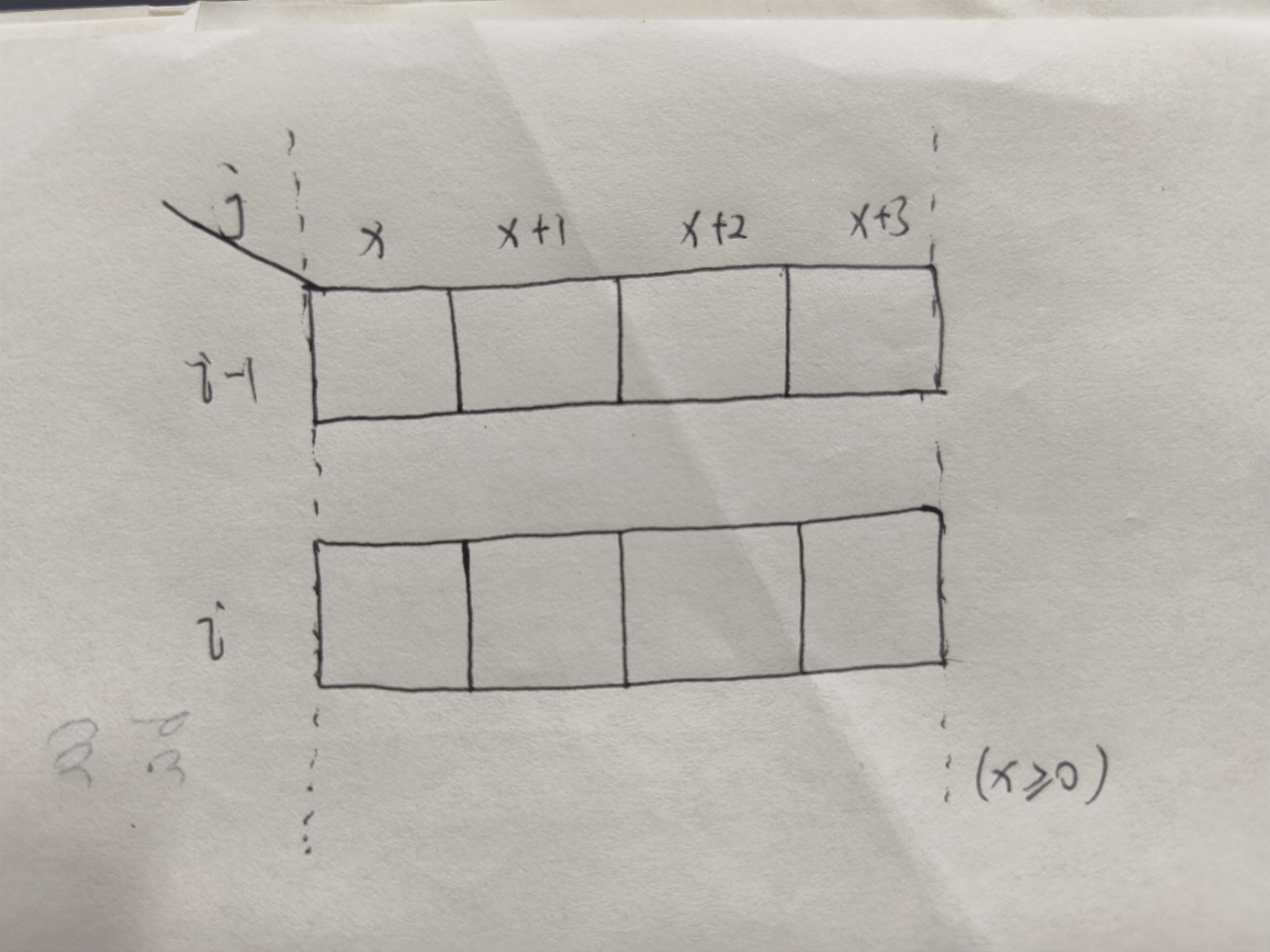
如果说第 i 层的数据的计算只是依赖于其竖直方向上对应的数据,那么我们的优化是没有问题的,
但是,通过上一张图片我们的计算过程模拟发现,并不是这样的,第 i 层数据的计算,有可能依赖
第 i - 1 层,其所在位置左上某个位置的数据的值,再具体一点,
就是假如我们现在计算到第 i 层数据 如果我们计算到第 i 层第 j 个数据,第 i 层第 j 个
数据的计算只是依赖于 第 i - 1 层,第 j 个数据的值,我们现在优化过后的代码没有问题,但是
第 i 层第 j 个数据的计算可能会依赖于第 i - 1 层,第 j - x 个数据的值,
现在这个代码优化之后的问题所在就是,如果出现这种 计算 第 i 层第 j 个数据时,依赖的是第
i - 1 层第 j - x 个数据,会给我们造成 一个错觉
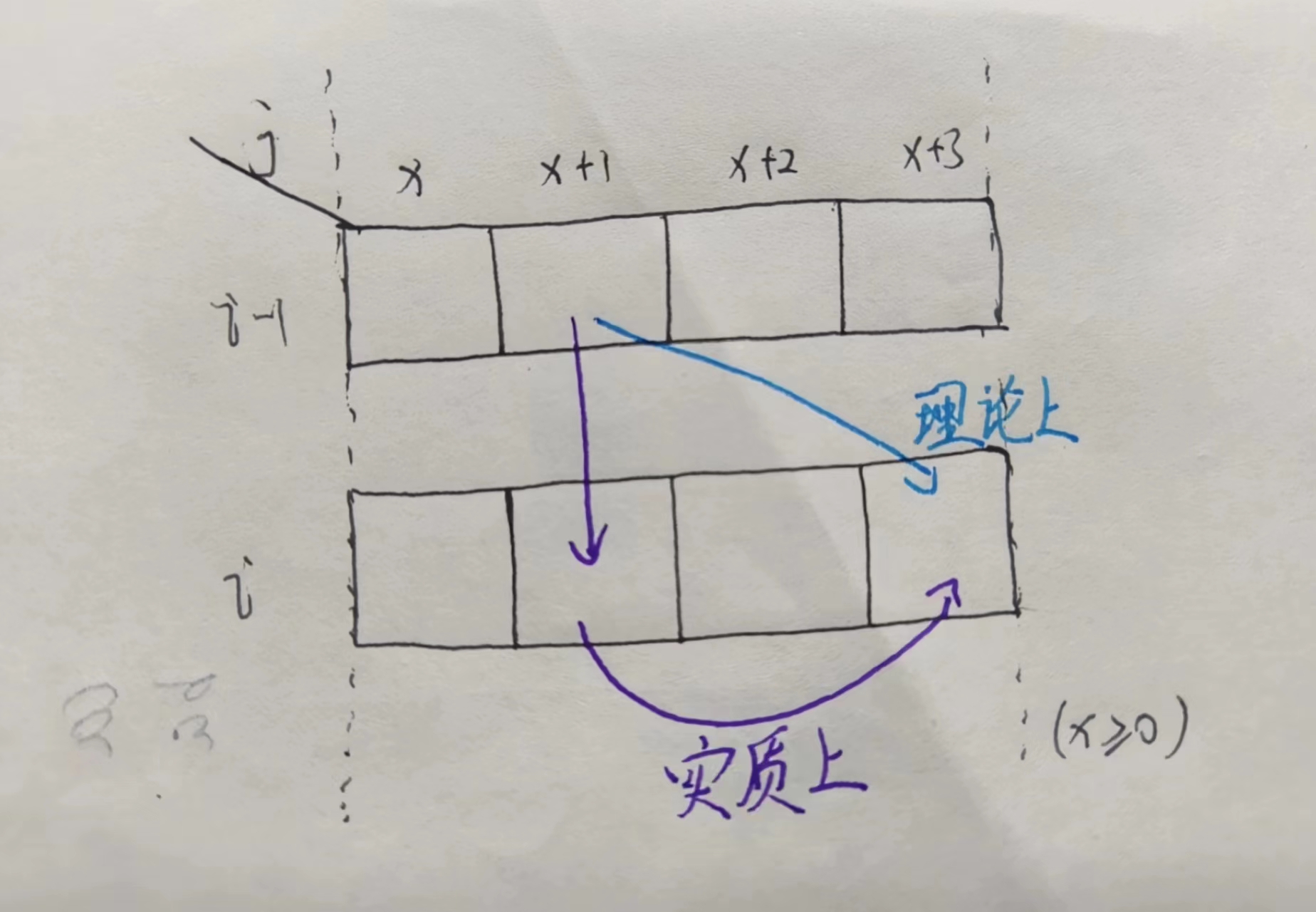
如图所示,就是如果说出现第 i 层某个数据的计算依赖的不是上一层其竖直方向对应的值,
我们优化后的代码其实是依赖的第 i 层数据的值,而不是第 i - 1 层数据的值,对此我们
如何解决这个问题呢,那就是给第二层循环倒序一下就可以了,核心代码就是这样
for (int i = 1; i <= n; i ++){
for (int j = m; j >= v[i]; j --){
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
一维版本代码展示
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N];
int v[N], w[N];
int main(){
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++){
for (int j = m; j >= v[i]; j --){
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
printf("%d\n", f[m]);
return 0;
}

