$\Huge\color{orchid}{点击此处获取更多干货}$

线性表出与扩展欧几里得算法

欧几里得算法就是求最大公约数的辗转相除法，这次来仔细看一下算法执行过程中发生了什么：

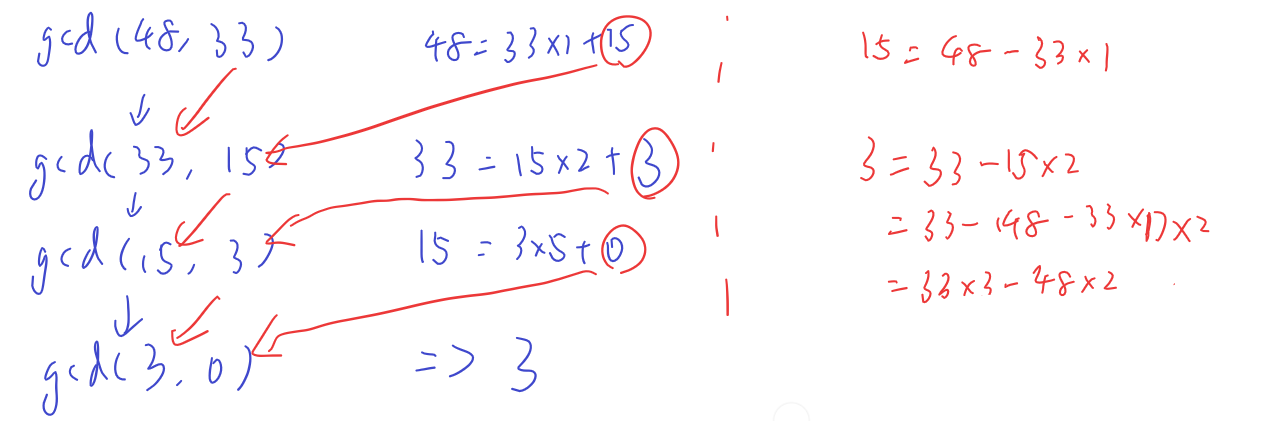
左侧蓝色部分代表每一轮的参数如何得到，将它们改写一下就是右边红色部分。在细说红色部分之前，先来介绍一下“线性表出”的概念

考研数学的线性代数中，向量组部分有这么一条定义：对于向量组$\{\vec{\alpha_1}, \vec{\alpha_2}, …, \vec{\alpha_n\}}$和同维度的向量$\vec{\beta}$，存在一组不全为0的数$\{k_1, k_2, …, k_n\}$，使得$\vec{\beta}={\textstyle \sum_{i=1}^{n}(k_i·\vec{\alpha_i})}$，则称向量组$\{\vec{\alpha_1}, \vec{\alpha_2}, …, \vec{\alpha_n\}}$可以线性表出向量$\vec{\beta}$，如果向量是1维的，则它们可以看成一个单独的数

然后再来看红色的每一行，$15=48-33*1$表示${48,33}$可以线性表出$15$，$3=33-15*2$表示${33,15}$可以线性表出$3$，而$gcd(48,33)$就是3.上述过程已经表明了${48,33}$可以线性表出它们的最大公约数$3$.由此，我们可以从任意的整数方程$a*x+b*y=gcd(a,b)$中找到${x,y}$的解

再用中间每一步的参数来线性表出一下它们的最大公约数，可得下图中绿色部分：

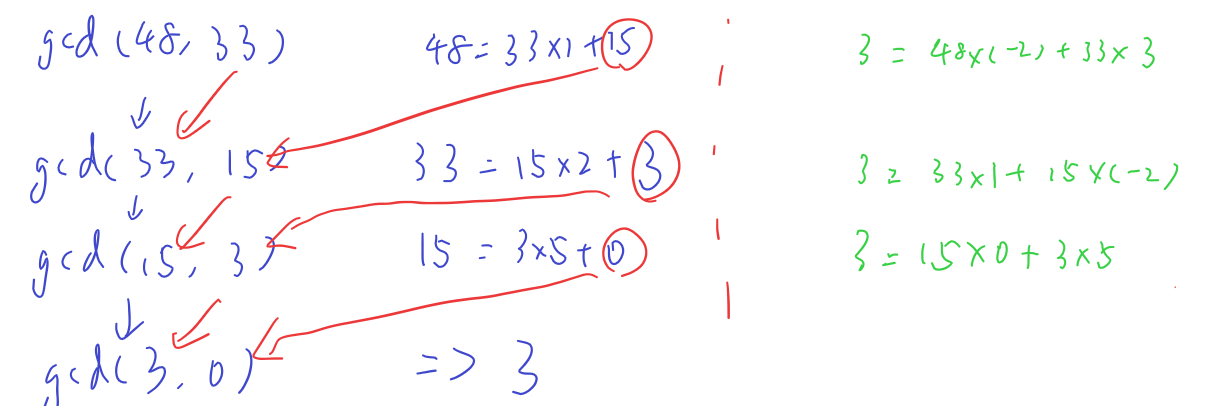
绿色部分正说明了求解$a*x+b*y=gcd(a,b)$相当于求解$b*x_0+(a\%b)*y_0=gcd(a,b)$，而$a\%b$在数学上的表示就是$a-b*\lfloor a/b \rfloor$，关于$a,b$合并同类项可得$a*y_0+b*(x_0-\lfloor a/b \rfloor*y_0)=gcd(a,b)$。在辗转相除的过程中不断地作$x=y_0,y=x_0-\lfloor a/b \rfloor*y_0$这样的变换，一直到$b=0$为止，此时对应的$x,y$分别为$1,0$

C++ 代码

/**
 * @brief 扩展欧几里得算法
 * @param a,b 待求gcd的一对数
 * @param x,y a*x+b*y=gcd(a,b)的解（引用传递）
 * @return gcd(a,b)
 * @warning x,y可能是负数，因此不能使用size_t类型
 */
int exGcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int d = exGcd(b, a % b, x, y), ox = x, oy = y;
    //自底向上变换
    x = oy;
    y = ox - (a / b) * oy;
    return d;
}