题目描述

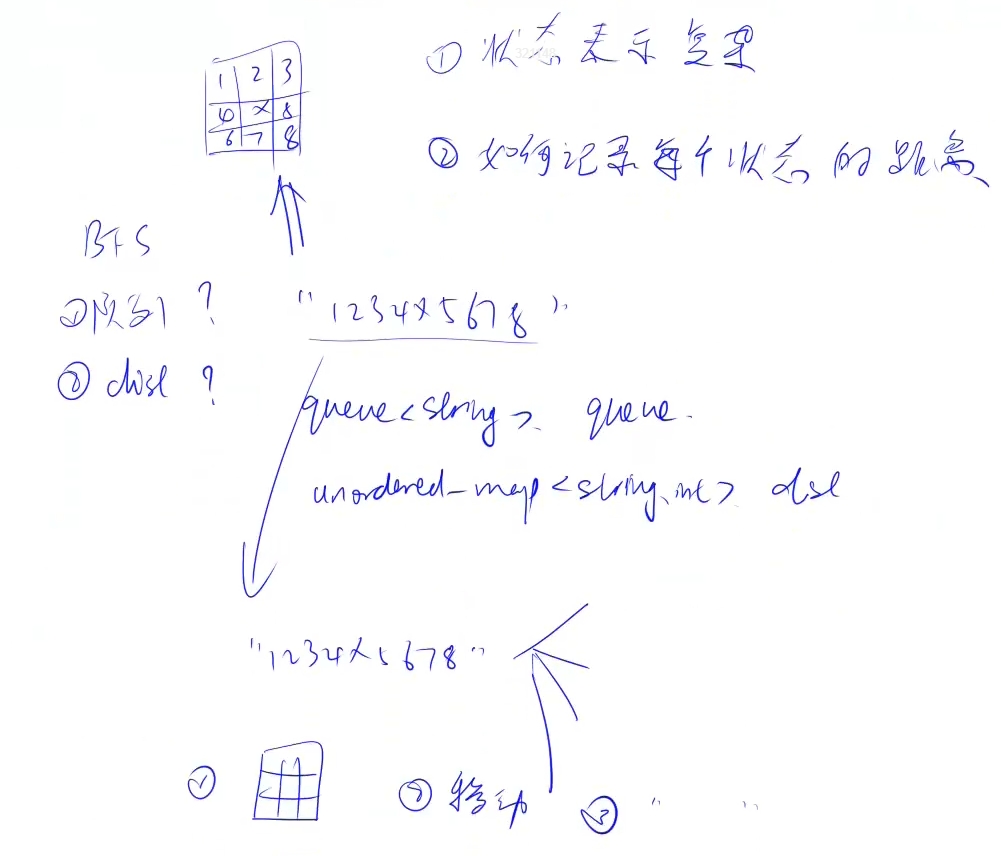
BFS：如何状态转移，如何存放当前的点距离起点的距离

//一维下标对应的二维下标转化公式:x2 = x1 / n y2 = x1 % m
//二维下标对应一维下标转化公式:x1 = x2 * n + y2
String newStr = new String(newState); //从char数组转化为String

样例

import java.util.*;

public class Main {
    static int bfs(String state) {

        //队列
        Queue<String> q = new LinkedList<>();
        //距离数组
        Map<String, Integer> d = new HashMap<>();

        //起点放入队列中
        q.offer(state);
        //(起点，起点到起点的距离为0）   某点到起点的距离可以认为成移动的次数 
        d.put(state, 0);

        //dx和dy代表偏移量数组 用来枚举上下右左四个方向
        int[] dx = {-1, 0, 1, 0};
        int[] dy = {0, 1, 0, -1};

        //终点(就是最后的状态)
        String end = "12345678x";

        while (!q.isEmpty()) {
            //拿到队首元素
            String t = q.poll();

            //如果队首元素等于终点 就返回终点到起点的距离(也就是移动了几次)
            if (t.equals(end))
                return d.get(t);

            //下面是状态转移

            //当前点(状态)距离终点的距离
            int distance = d.get(t);

            //找到当前x的位置
            int k = t.indexOf('x');
            //一维下标对应的二维下标转化公式:x2 = x1 / n  y2 = x1 % m   
            //二维下标对应一维下标转化公式:x1 = x2 * n + y2
            int x = k / 3, y = k % 3;

            //枚举上下右左四个方向
            for (int i = 0; i < 4; i++) {

                int a = x + dx[i], b = y + dy[i];

                //a和b不越界，
                if (a >= 0 && a < 3 && b >= 0 && b < 3) {

                    //更新状态(由于我们这相当于新生成了一个字符串 所以不需要还原状态了)
                    char[] newState = t.toCharArray();
                    //二维下标对应一维下标转化公式:x1 = x2 * n + y2
                    char temp = newState[a * 3 + b];
                    newState[a * 3 + b] = newState[k];
                    newState[k] = temp;
                    //不能用newState.toString(); 
                    String newStr = new String(newState); 


                    //如果这个状态之前没有被搜到过
                    if (!d.containsKey(newStr)) {
                        //把这个新的状态放入，并且距离起点的距离加1(也就是移动次数+1)
                        d.put(newStr, distance + 1);
                        //扩展队首
                        q.add(newStr);
                    }

                }
            }
        }

        return -1;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        //读进来的字符串，也就是起点(初始状态)
        String state = "";
        for (int i = 0; i < 9; i++) {
            state += scanner.next();
        }

        System.out.println(bfs(state));
    }
}