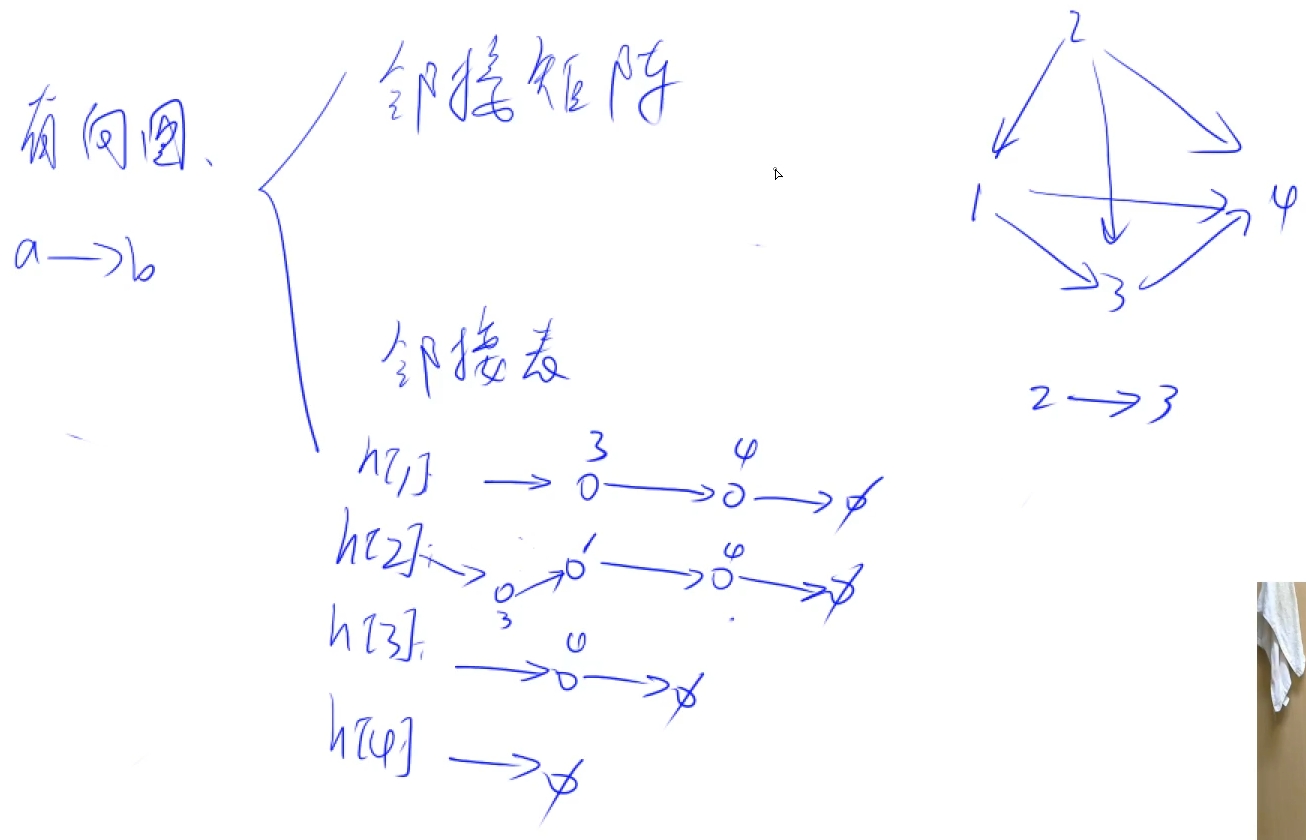
初始化树或图的临接表的代码

dfs去搜树或图(每个点只会搜一次)

dfs无法求最短路

import java.util.*;

public class Main {
    static final int N = 100010, M = N * 2;
    //头数组
    static int[] h = new int[N];
    //存储每个结点的值
    static int[] e = new int[M];
    //存储每个结点的next指针
    static int[] ne = new int[M];
    //当前用了多少个点
    static int idx;
    //判断一下该点是否被搜索过 dfs搜点 只搜一遍
    static boolean st[N];

    //例如存储a->b 这条边 我们是在首位置插入
    static void add(int a, int b) {
        //先把b的值赋上
        e[idx] = b;
        //当前数的next指针指向原本的头结点
        ne[idx] = h[a];
        //头指针指向当前位置 idx加1
        h[a] = idx++;
    }

    //搜树或图
    static void dfs(int u){
        //标记当前的点已经被搜过了
        st[u] = true;

        //遍历u的所有出边 (跟遍历单链表差不多)
        //从头结点开始遍历，如果当前位置不是-1，则继续遍历ne[i]
        for(int i = h[u]; i != -1 ; i = ne[i]){
            //j存储当前链表的结点指向的下一个结点对应图（在树里面，也就是儿子）里面的编号是多少
            int j = e[i];
            //如果当前点没有被搜索过 ，就继续向下搜索
            if(!st[j])dfs(j);
        }
    }

    public static void main(String[] args) {
        Arrays.fill(h, -1);

        //比方从第一个点开始搜索
        dfs(1);
    }
}

题目描述

先把删除每个点后连通块的最大点数都求出来，再看这些最大里面最小的那个数，就找到树的重心
等价于找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

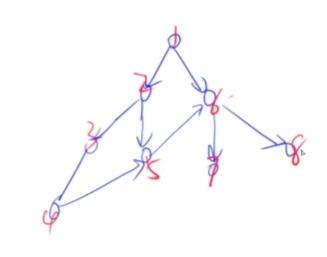
例如下图：删除根结点，连通块的最大点数为4

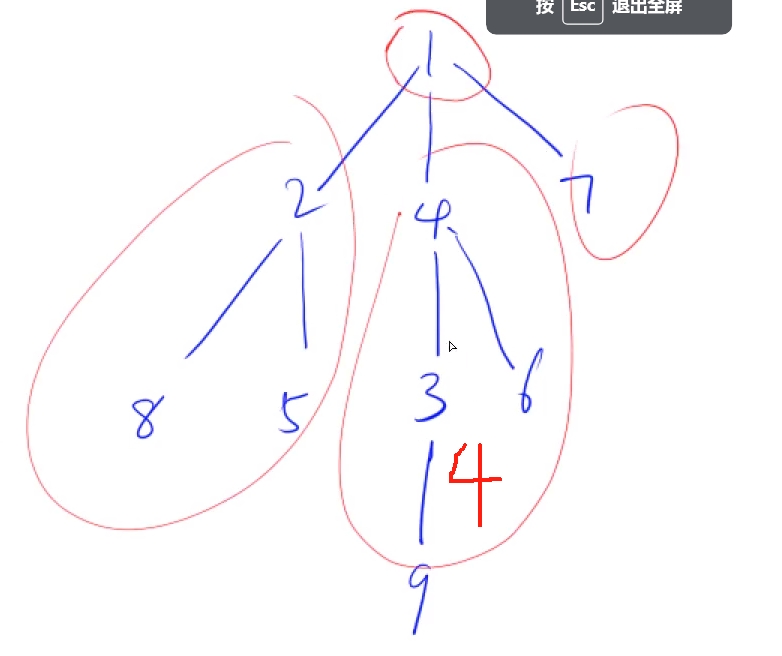
问题就算换到如何去求子树的大小，dfs就可以。
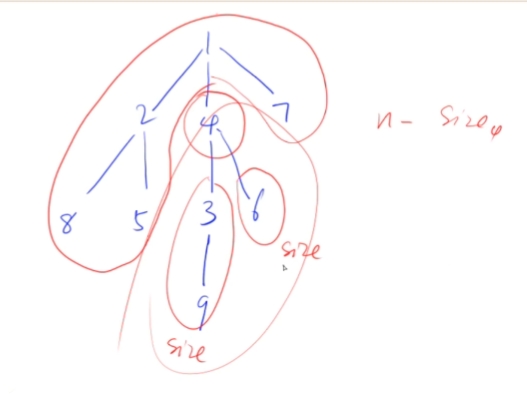
对于删除某个点，分成了几个连通块，我们依据下图可以看到。对于4这个结点的每个子树都会构成一个连通块，剩余的部分组成一个连通块。对于剩余的部分组成的连通块的点数= n - 点4的子树大小

import java.util.*;

public class Main {
    static final int N = 100010, M = N * 2;
    //头数组
    static int[] h = new int[N];
    //存储每个结点的值
    static int[] e = new int[M];
    //存储每个结点的next指针
    static int[] ne = new int[M];
    //当前用了多少个点
    static int idx;
    //判断一下该点是否被搜索过 dfs搜点 只搜一遍
    static boolean[]  st= new boolean[N];

    //最终答案 最大值的最小值
    static int ans = N;

    static int n;

    //例如存储a->b 这条边 我们是在首位置插入
    static void add(int a, int b) {
        //先把b的值赋上
        e[idx] = b;
        //当前数的next指针指向原本的头结点
        ne[idx] = h[a];
        //头指针指向当前位置 idx加1
        h[a] = idx++;
    }

    //搜树或图
    static int dfs(int u){
        //标记当前的点已经被搜过了
        st[u] = true;

        //sum代表子树的大小。最小为1，res代表删除某个结点（u）的每个子树都会构成一个连通块的点数的最大值.
        int sum = 1,res = 0;

        //遍历u的所有出边 (跟遍历单链表差不多)
        //从头结点开始遍历，如果当前位置不是-1，则继续遍历ne[i]
        for(int i = h[u]; i != -1 ; i = ne[i]){
            //j存储当前链表的结点对应图（树）里面的编号是多少
            int j = e[i];
            //如果当前点没有被搜索过 ，就继续向下搜索
            if(!st[j]){
                //表示当前结点子树的大小
                int s = dfs(j);
                //删除某个结点的每个子树都会构成一个连通块的点数的最大值
                res = Math.max(res , s);
                //当前这个结点的子树是以(删除)u为结点的子树，所以要统计一下
                sum += s;
            }
        }

        //比较剩余的部分组成一个连通块的点数 与 删除某个结点（u）的每个子树都会构成一个连通块的点数的最大值，谁大
        res = Math.max(res , n - sum);

        //System.out.println(ans +" " + res);

        //找最大值的最小值
        ans = Math.min(ans,res);

        //返回当前结点子树的大小
        return sum;

    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        Arrays.fill(h, -1);

        //结点为n 边只有n-1条 所以循环条件为n-1
        for(int i = 0; i < n - 1; i++){
             int a = sc.nextInt();
             int b = sc.nextInt();

             //由于是无向图 a->b和b->a都得存
             add(a,b);add(b,a);

        }


        //从第一个点开始搜索
        dfs(1);

        System.out.println(ans);
    }
}