题目描述
最简分数:分子与分母互质的数
算法1
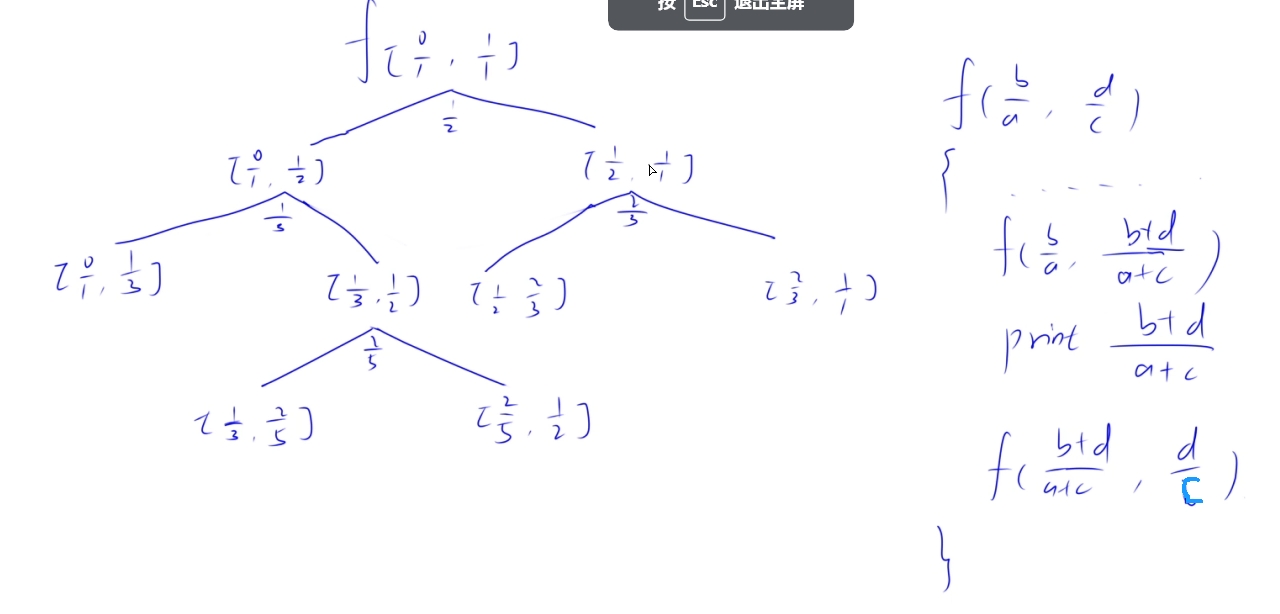
Stern-Brocot Tree O(n2)
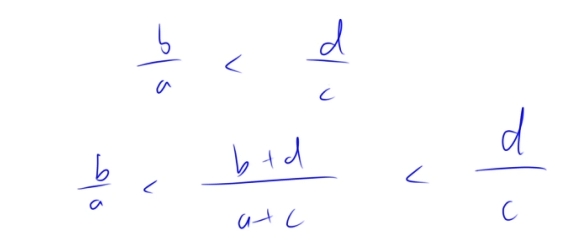
import java.util.*;
public class Main{
/*
利用Stern–Brocot树 其实就是 a/b < a+c/b+d < c/d 对分成的两个区间,不断得去找中间值
*/
static int n;
static void dfs(int a,int b,int c,int d){
if(b + d > n) return;
dfs(a,b,a+c,b+d);
System.out.print(a+c);
System.out.print("/");
System.out.print(b+d);
System.out.println();
dfs(a+c,b+d,c,d);
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
System.out.println("0/1");
dfs(0,1,1,1);
System.out.println("1/1");
}
}
算法2
暴力做法 O(n2logn)
import java.util.*;
/*
最简分数:分子与分母互质的数
*/
public class Main {
static class Fraction {
int x, y;
//y是分子 x是分母
Fraction(int x, int y) {
this.x = x;
this.y = y;
}
}
//找最大公约数
static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
ArrayList<Fraction> fractions = new ArrayList<>();
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= i; j++) {
//如果最大公约数为1,说明它们互质,且分子 < 分母,符合条件
if (gcd(i, j) == 1) {
fractions.add(new Fraction(i, j));
}
}
}
//排序 a.y/a.x > b.y/b.x 返回值大于0升序 返回值小于0降序
fractions.sort((a, b) -> a.y * b.x - a.x * b.y);
for(Fraction fraction : fractions) {
System.out.println(fraction.y + "/" + fraction.x);
}
}
}

