$\Huge\color{orchid}{点击此处获取更多干货}$

匈牙利算法

二分图匹配问题中，从时间效率上来说，匈牙利算法并不是最优解。但既然基础篇中这个问题的算法标签是“匈牙利算法”，那么还是给点面子介绍一下吧，至于问题的最优解算法，它使用的模型跟匈牙利算法有些相通之处，这些等到提高篇再说

匈牙利算法的提出者是匈牙利科学家Edmonds，因此得名“匈牙利算法”，核心思想就是“增广路”的寻找（留意这两个加粗的名字，提高篇另一种模型中还会遇到这些）。下面来图解一下如何增广，即如何寻找匹配：

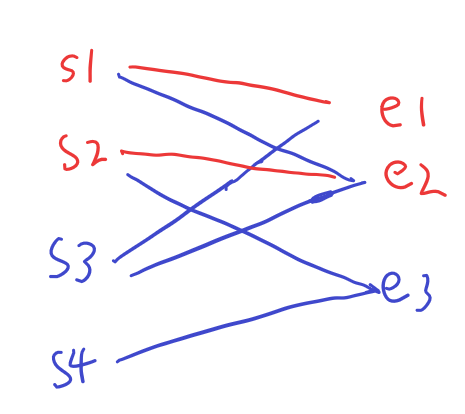
刚开始所有节点都未匹配，此时先将$s_1$和$e_1$，$s_2$和$e_2$这两对显然的配成对。但是到$s_3$的时候，其后继$e_1$和$e_2$都已经被匹配了，陷入了死局，此时只产生了两对匹配，但是很明显，这样的图中可以有3对匹配。这时就引入了一个重要操作：回退

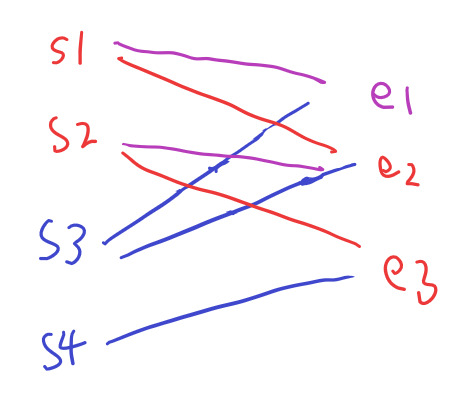
$s_3$的后继$e_1$原本和$s_1$成对，这时回退掉$e_1$，$s_1$需要和另一个后继$e_2$匹配，但$e_2$也和$s_2$配对着，那么再回退掉$e_2$，$s_2$就可以找空闲的后继$e_3$配对，把$e_2$留给刚刚回退的$s_1$。最后，$s_3$和$e_1$配对，这样就成功找到了3对匹配

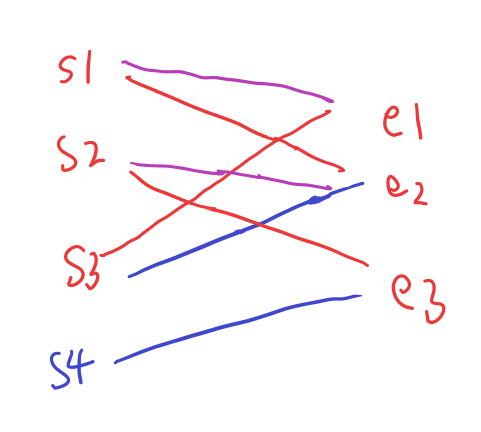
此时还剩一个$s_4$，但是如果让$s_4$匹配$e_3$，回退的时候再次让$s_1,s_2$的配对节点成为$e_1,e_2$，会发现$s_3$的两个后继都被其他节点匹配着，无法再增加匹配数。

上述寻找匹配的操作就叫“增广”，每次增广成功的特点就是匹配数增加了1，因此最大匹配数就相当于增广成功的次数。

C++ 代码

实现方面，三种存储方式也都可以用于存储二分图，此帖仍然以链式前向星为例
二分图类定义：

class BipartiteGraph {
private:
    size_t* fin, * last, * pre,         //链式前向星的各表，last为左半区节点所用
        * vis,                          //右半区节点访问记录
        * mate;                         //右半区节点在左半区中配对的节点序号
    int leftSize, rightSize, numArc,    //左右半区的节点数量和边数量
        tot = 1;                        //边的插入位序

    void connect(int s, int e);         //连接两个节点

    bool match(int x);                  //尝试为左半区节点配对
public:
    BipartiteGraph(int nl, int nr, int m);//构造函数
    ~BipartiteGraph();                  //析构函数

    size_t maxPairs();                  //求最大匹配数
};

构造函数：

/**
* @brief 二分图类的构造函数
* @param nl 左半区节点数
* @param nr 右半区节点数
* @param m 边数 
* 构造一个m条边的二分图，其左半区含nl个节点，右半区含nr个节点
*/
BipartiteGraph::BipartiteGraph(int nl, int nr, int m)
{
    leftSize = nl;
    rightSize = nr;
    numArc = m;
    //如果分不清表为左右哪个半区所用，可以用max(leftSize,rightSize)+1做表长
    fin = new size_t[numArc + 5];
    last = new size_t[leftSize + 1]();
    pre = new size_t[numArc + 5];
    vis = new size_t[rightSize + 1]();
    mate = new size_t[rightSize + 1]();
    while (m--) {
        int s, e;
        cin >> s >> e;
        connect(s, e);//无论是从哪个半区开始向另一个半区匹配都是一样的，因此可以只做单向连接
    }
}

析构函数就是delete掉那些表，不用多说

单向连接：

/**
* @brief 连接两个节点
* @param s 起点
* @param e 终点
* 从左半区的节点s向右半区的节点e连接一条边（链式前向星单向连接）
*/
void BipartiteGraph::connect(int s, int e)
{
    fin[tot] = e;
    pre[tot] = last[s];
    last[s] = tot++;
}

增广（寻找匹配）：

/**
* @brief 为左半区节点配对
* @param x 寻找匹配的起点
* @retval true 配对成功
* @retval false 配对失败
* 以递归方式从左半区节点x开始，用增广路思想寻找其配对节点
*/
bool BipartiteGraph::match(int x)
{
    for (int i = last[x]; i != 0; i = pre[i]) {
        int nx = fin[i];
        if (vis[nx]) {
            //右半区节点必须是未访问状态
            continue;
        }
        vis[nx] = 1;
        if (mate[nx] == 0 || match(mate[nx])) { 
            //将右半区nx与左半区x配对的条件有两个
            //一是nx未配对，二是nx原先的配对节点还有其他配对可能性
            mate[nx] = x;
            return true;
        }
    }
    return false;
}

获取最大匹配数：

/**
* @brief 获取最大匹配数
*/
size_t BipartiteGraph::maxPairs()
{
    size_t cnt = 0;
    for (int i = 1; i <= leftSize; i++) {   
        fill(vis, vis + rightSize, 0);  //左半区每个节点在开始匹配时，右半区的节点都视作未访问
        if (match(i)) {                 //每次尝试增加一对，成功就累加到总数上
            cnt++;
        }
    }
    return cnt;
}

备注

匈牙利算法的时间复杂度是$O(n*m)$，$n$是左半区节点数量，$m$是边的总数，这样的时间复杂度还有提升空间。提高篇中，会将“网络流”模型运用于其中，通过多次优化，最终的时间复杂度可以降到$O(\sqrt{n}*m)$。此外，还有个冷门的HK算法，时间复杂度也是$O(\sqrt{n}*m)$，不作为基础篇的内容公开介绍，有兴趣者自行了解