$\Huge\color{orchid}{点击此处获取更多干货}$

二分图定义及判定方法

二分图在离散数学中出现过，其定义为：
无向图$G(V,E)$中，能把所有节点分为两个非空集合$V_a,V_b$，对于每条边$\{s,e\}$，两个顶点$s$和$e$都一定分别属于$V_a,V_b$两个集合
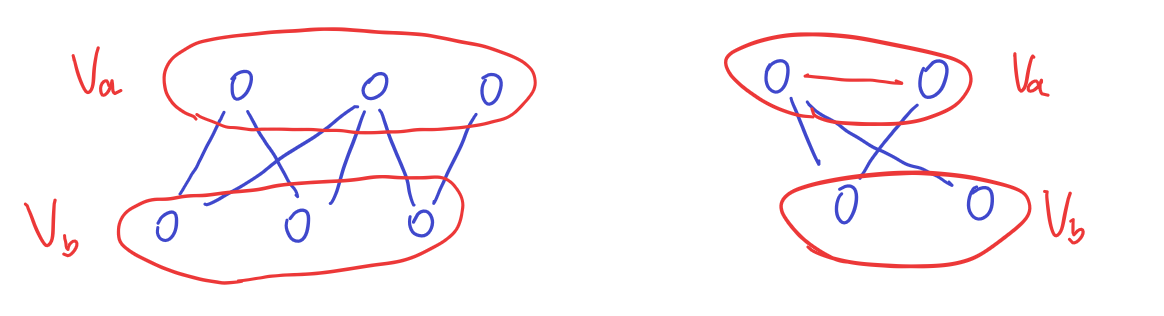
如下图，左边的就是二分图，而右边的不是二分图

由上述定义，还可以推出三个性质：
1. 图中至少要有两个节点
2. 两个节点集合内部，不存在任意两个直接相连的节点
3. 图结构内部不存在节点数量为奇数的回路

判断二分图有一个很直接的方式：为每个节点染色
染色的规则如下：
1. 用两种颜色为节点染色
2. 如果某节点被染成了其中一种颜色，那么其后继节点都应当为另一种颜色，不存在两个直接相连的同色节点

在染色的过程中，将某一节点染成一种颜色后，其后继节点的染色情况有以下3种：
1. 无色：染成不相同的另一种颜色
2. 同色：说明出现了节点数量为奇数的回路，此时直接判断false
3. 异色：继续考虑此节点的后继情况，直到所有节点都被染上色且没有出现情况2

此染色过程可以用DFS也可以用BFS，三种一般的图结构存储方式都可以使用，下面以链式前向星为例（忘了的话看这里），假设类内已经定义好了各节点颜色表$\text{color}$（初始全0），染色的成员函数$\text{setColor}$和判断二分图的成员函数$\text{isBipartite}$

C++ 代码

染色（DFS）：

/**
* @brief 按照DFS方式染色
* @param cur 当前即将染色的节点
* @param c 即将染上的颜色
* 从当前节点开始，向后继节点搜索并判断染色是否合法
* 
* @retval true 染色合法
* @retval false 染色不合法，即出现节点数为奇数的回路
* 
* @warning 参数color只能是1或-1
*/
bool LinkGraph::setColor(int cur, int c) {
    color[cur] = c;
    for (int i = last[cur]; i != 0; i = pre[i]) {
        int nx = fin[i];
        if (color[nx] == 0) {           //没有染色，就用递归方式去染色
            if (!setColor(nx, -c)) {
                return false;
            }
            else if (color[nx] == c) {  //相同颜色，直接返回false
                return false;
            }
            //不同颜色，直接跳过
        }
    }
    return true;
}

染色（BFS）：

/**
* @brief 按照BFS方式染色
* @param 同DFS方式
* 详细内容也同DFS方式
* @note 参数c在BFS方式中可有可无，带上是为了减少isBipartite函数的改动
*/
bool LinkGraph::setColor(int cur, int c) {
    queue<pair<int, int>> q;
    q.push({cur, c});
    while (!q.empty()) {
        auto node = q.front();
        q.pop();
        int curPos = node.first, curColor = node.second;
        color[curPos] = curColor;
        for (int i = last[curPos]; i != 0; i = pre[i]) {
            int nxtPos = fin[i];

            //BFS方式下更明显
            if (!color[nxtPos]) {                   //未染色就染色
                color[nxtPos] = -curColor;
                q.push({nxtPos, color[nxtPos]);
            }
            else if (color[nxtPos] == curColor) {   //已经同色就false
                return false;
            }
            //异色的跳过
        }
    }
    return true;
}

二分图判断：

/**
* @brief 判断此图是否为二分图
* 无需参数，因为节点总数已在类内保存
*/
bool LinkGraph::isBipartite() {
    for (int i = 1; i <= numVex; i++) {
        if (color[i] == 0) {            //未染色
            if (!setColor(i, 1)) {      //没有合法染色方式
                return false;           //只要有一个节点出现这样的问题就返回false
            }
        }
    }
    return true;
}