$\Huge\color{orchid}{点击此处获取更多干货}$

完全二叉树与堆

完全二叉树在前置知识中提过，它的每个节点都和相同层数的完美二叉树节点位置相同。那么如果我们从根到叶，从左到右的为每个节点标号，就可以用序列来存放树的节点。标号的规则主要有两条：
1. 根节点标号为1
2. 任意一个标号为$x$的节点，如果其含有左孩子，标$2*x$，如果其含有右孩子，标$2*x+1$

用$v_x$表示标号$x$的树节点中有效的元素，如果这样的序列在某种比较规则下，对于任意的$v_x$都满足$v_x > v_{2*x}, v_x > v_{2*x+1}$，或者是$v_x < v_{2*x}, v_x < v_{2*x+1}$，这样的序列就是堆，前者为大顶堆，后者为小顶堆。（下面全都以大顶堆为例）

基本的堆操作为插入$(\text{push})$，删除$(\text{pop})$，取顶部$(\text{top})$。由于以任意次序插入的元素中，都只有最大的才最先出，因此和其他序列式结构不同，堆的元素进出性质是$\text{RIMO(Random In Maximum Out)}$也就是“任意进，最大出”

本次的需求中还有两条非常规操作，即对“第k次插入的元素”执行删除和修改。之前在链表部分见过的“插入位序”，在此处可以继续用上。接下来结合代码，介绍各操作的原理

C++代码

堆在STL中以优先队列$\text{(priority_queue)}$出现，有3个模板参数：元素类型，容器类型，排序规则。考虑到实际使用中容器类型大多数为vector，这一个参数在此处省略。下面是类定义：

/**
* @brief 包含元素和插入位序的节点
* 在PriorityQueue类中作为堆本身存储的对象使用
*/
template<class Elem>
struct HeapNode {
    Elem val = Elem();  //元素自身
    size_t insIdx = 0;  //该元素对应的插入位序
    HeapNode() {}
    HeapNode(Elem e, size_t id) : val(e), insIdx(id) {}

    /**
    * @brief 比较运算符重载
    * @param node 待比较的对象
    * 
    * @retval true 大于
    * @retval false 小于或等于
    */
    bool operator>(const HeapNode<Elem>& node) const {
        return this->val > node.val;
    }
};

/**
* @brief 仿照STL定义的堆（优先队列）模板类
* @param Elem 堆中的元素类型
* @param Pred 堆中元素的排序规则
* 
* 和STL一样为大顶堆，不过此处默认排序规则不是STL默认的less而是greater
*/
template<class Elem, class Pred = greater<Elem>>
class PriorityQueue {
private:
    vector<HeapNode<Elem>> base;    //堆结构本体
    vector<size_t> pos;             //下标为k的元素代表插入位序k的节点在堆中的位置（有效值从1开始）
    Pred pred;                      //排序规则，结构体仿函数，事先构造
    size_t size = 0;                //堆的大小
    size_t idx = 1;                 //下一个元素的插入位序

    void adjustUp(size_t id);       //向上调整
    void adjustDown(size_t id);     //向下调整
public:
    PriorityQueue();                //构造函数
    void push(Elem e);              //插入操作（一般）
    void pop();                     //删除操作（一般）
    Elem top();                     //取顶部操作（一般）
    void eraseKthElement(size_t k);         //按插入位序删除元素（特殊）
    void updateKthElement(size_t k, Elem e);//按插入位序更新元素（特殊）
};

构造函数：

/**
* @brief 模板类构造函数
* 为base和pos两表增加+1的偏移，使起始位置统一为1
*/
template<class Elem, class Pred>
PriorityQueue<Elem, Pred>::PriorityQueue()
{
    base.push_back(Elem());
    pos.push_back(0);
}

插入操作：

/**
* @brief 堆插入操作
* @param e 待插入的元素
* 先在base和pos表尾插入对应类型的元素，然后向上调整维持堆性质
*/
template<class Elem, class Pred>
void PriorityQueue<Elem, Pred>::push(Elem e)
{
    base.push_back(HeapNode<Elem>(e, idx));
    pos.push_back(idx);
    size++;
    adjustUp(idx);
    idx++;
}

插入中最重要的就是“向上调整”，带上了插入位序后，注释中也许无法解释清楚了，先上图：

初始状态如图所示，红色的是数值，绿色的是插入位序，右边是类内各表内容。现在我们插入87（插入位序是7），然后看一下向上调整之后，各表发生了怎样的变化：

less排序规则代表着大标号元素需要比小标号元素小，所以从当前的标号7开始，向标号更小的方向寻找不符合当前排序规则的元素节点。原先标号3的71比87小，因此需要将71和87对应的节点交换，除此之外还需要根据两元素的插入位序，在pos表中找到它们原先在堆中的位置，并把这个也交换。在交换后，插入位序为7的87在标号3的位置，原先其标号7的位置被插入位序6的71代替。再往上走，标号1的98比87大，因此不动。
向上调整$\text{(adjustUp)}$函数的代码如下：

/*
* @brief 向上调整，以维护堆性质
* @param id 调整的起始位置
* 交换时base和pos对应元素都要交换，注释篇幅有限请见文档
*/
template<class Elem, class Pred>
void PriorityQueue<Elem, Pred>::adjustUp(size_t id)
{
    size_t cur = id;
    while (cur > 1) {                       //需要在cur = 1时退出
        //greater排序规则正相反，大标号元素大于小标号元素
        if (!pred(base[cur].val, base[cur / 2].val)) {
            size_t curIdx = base[cur].insIdx, nxtIdx = base[cur / 2].insIdx;
            swap(base[cur], base[cur / 2]); //换元素值和插入位序
            swap(pos[curIdx], pos[nxtIdx]); //取出两元素在堆中的位置，交换
            cur /= 2;                       //上移 
        }
        else {
            break;
        }
    }
}

然后是删除，这里先说一般的从堆顶删除($\text{pop}$)，它分3步：
1. 将堆顶元素的插入位序置为0（pos中也修改），并和尾部元素互换
2. 将已经置于尾部的待删除元素从base中删除，保留pos上的插入位序
3. 从堆顶开始向下调整，维护堆性质

/**
* @brief 堆顶删除操作
* 交换base首尾节点，pos中也做更改，然后删除base的末尾
*/
template<class Elem, class Pred>
void PriorityQueue<Elem, Pred>::pop()
{
    size_t delPos = base[1].insIdx, endPos = base[size].insIdx;
    pos[endPos] = 1;
    pos[delPos] = 0;
    swap(base[1], base[size]);
    base.pop_back();
    size--;
    adjustDown(1);
}

这里面也有一个比较重要的“向下调整”成员函数$adjustDown$，同样图示说明：

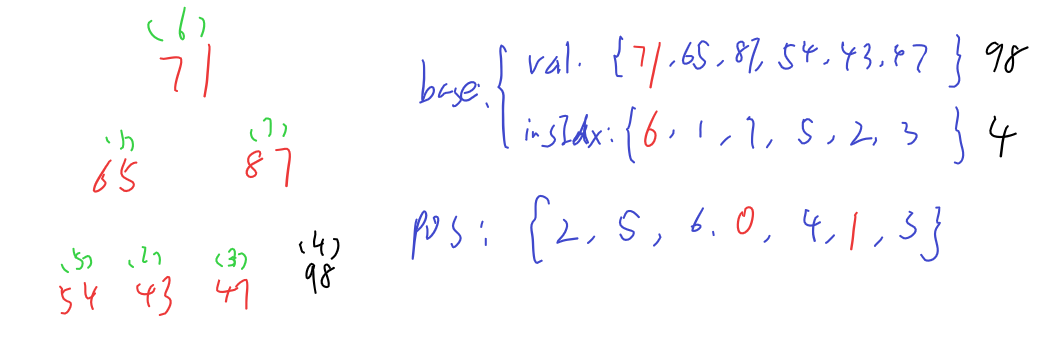
这是堆顶98被删除之后的情况，被删的98已被标黑，其插入位序4保留下来，但是由于此98已经不在堆中，pos表中插入位序4的元素在堆中的位置就用0来表示“不存在”，同时原先的71来到顶端，其插入位序为6，在堆中的位置变为1。这时从位置1开始向下调整，下一个待交换的可能有两种选项：
1. 如果该节点存在左孩子，并且在当前排序规则下，左孩子的元素值靠后，就和左孩子交换
2. 如果该节点左右孩子都存在，并且右孩子的值比左孩子和自身都靠后，就和右孩子交换

由于一个节点不可能只存在右孩子不存在左孩子（完全二叉树结构限制），故可以先将下一层待交换的元素视为当前元素的左孩子，然后按照选项2检查是否该和右孩子交换。代码如下：

/**
* @brief 向下调整，维护堆性质
* @param id 调整的起始位置
* 交换同adjustUp，还有一些额外细节写在行注释中
*/
template<class Elem, class Pred>
void PriorityQueue<Elem, Pred>::adjustDown(size_t id)
{
    size_t cur = id, nxt = 2 * id;
    while (nxt <= size) {
        //能进这里的循环，就说明左孩子存在
        if (nxt + 1 <= size
            && !pred(base[nxt + 1].val, base[nxt].val)) {
            //进入这里说明右孩子存在且值比较靠后，那么待交换的就是右孩子
            nxt++;
        }
        if (!pred(base[nxt].val, base[cur].val)) {  //这里就跟向上调整是一样的了
            size_t curIdx = base[cur].insIdx, nxtIdx = base[nxt].insIdx;
            swap(base[nxt], base[cur]);
            swap(pos[curIdx], pos[nxtIdx]);
            cur = nxt;
            nxt = 2 * cur;
        }
        else {
            break;
        }
    }
}

取堆顶就很简单了，既然完全二叉树根节点标号是1，那么堆顶就是1位置的节点代表的元素

/**
* @brief 取堆顶
* 根据堆的性质，显而易见了
*/
template<class Elem, class Pred>
Elem PriorityQueue<Elem, Pred>::top()
{
    return base[1].val;
}

以上就是堆结构的一般操作，为避免本帖篇幅过长，两种特殊操作以及排序功能在下篇