题目描述

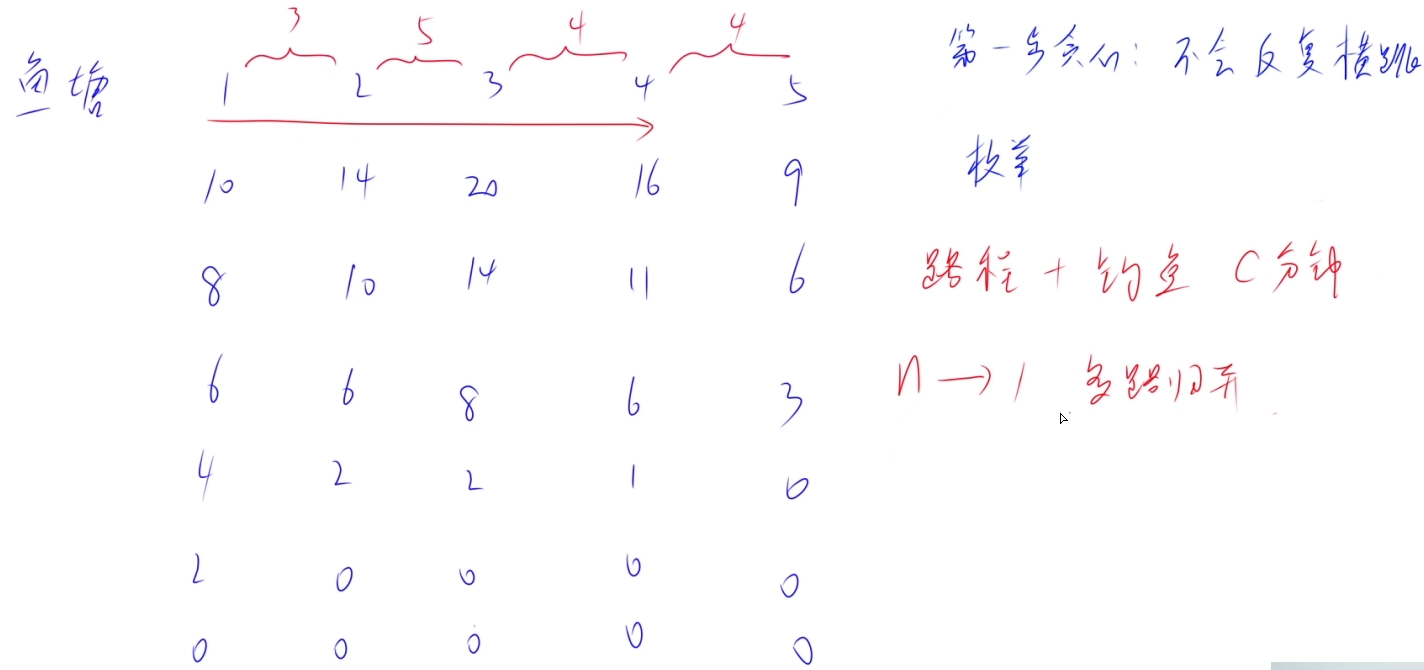
贪心+多路归并

样例

import java.util.*;

/*
   多路归并+贪心

   贪心：1.分为拐弯和不拐弯，我们可以发现不拐弯最好。因此得出有n条线路，1至1，1至2 ... 1至n, 共有n条路线

   多路归并：每次去找当前时间在哪个鱼塘能钓最多的鱼，依次相加

*/

public class Main {
    static final int N = 110;
    //a表示第一次钓的鱼数 d表示每分钟减少的鱼数  t表示两个鱼塘的距离  spend表示在这个鱼塘花费了多少时间
    static int[] a = new int[N], d = new int[N], t = new int[N], spend = new int[N];
    static int n;

    //计算当前鱼塘能钓多少鱼
    public static int get(int x) {
        //要和0取个最大，因为钓鱼不能是负数
        return Math.max(0, a[x] - d[x] * spend[x]);
    }

    public static int work(int x, int s) {
        int sum = 0;
        //先把spend清空
        Arrays.fill(spend, 0);
        //找出当前时间最大的钓鱼数量
        for (int i = 1; i <= s; i ++) {
            int tmp = 1;
            for (int j = 1; j <= x; j ++) 
                //在当前时间哪个鱼塘能钓最多的鱼
                if (get(j) > get(tmp))
                    tmp = j;//赋值给tmp
            sum += get(tmp);//sum+=当前时间哪个鱼塘能钓最多的鱼
            spend[tmp] ++;//当前时间哪个鱼塘能钓最多的鱼对应的鱼塘花费时间加1
        }
        return sum;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for (int i = 1; i <= n; i ++) a[i] = sc.nextInt();
        for (int i = 1; i <= n; i ++) d[i] = sc.nextInt();
        // t[i]表示走到第i个鱼塘总共花的时间 直接预处理成前缀和
        for (int i = 2; i <= n; i ++) t[i] = t[i - 1] + sc.nextInt();
        int T = sc.nextInt();
        int res = 0;
        //枚举每一个路线用T - t[i]来钓鱼的时间，所获得的鱼数.
        for (int i = 1; i <= n; i ++) res = Math.max(res, work(i, T - t[i]));
        System.out.println(res);
    }
}