本题贪心思路可参考其它题解
本篇题解只解释代码上的一个细节问题
一般贪心代码如下:
#include <algorithm>
using namespace std;
const int N = 100005;
int n, res;
int a[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
for (int i = 0; i < n; i ++ ) res += abs(a[i] - a[n >> 1]);
printf("%d\n", res);
return 0;
}
该代码第 17 行中,将 abs(a[i] - a[n >> 1]) 改为 abs(a[i] - a[i >> 1]) 也可以 AC
注意这并不是数据的锅,我们可以证明排序之后,有 n−1∑i=0|ai−an2|=n−1∑i=0ai−ai2
下面贴一份证明过程(来自 yxc)
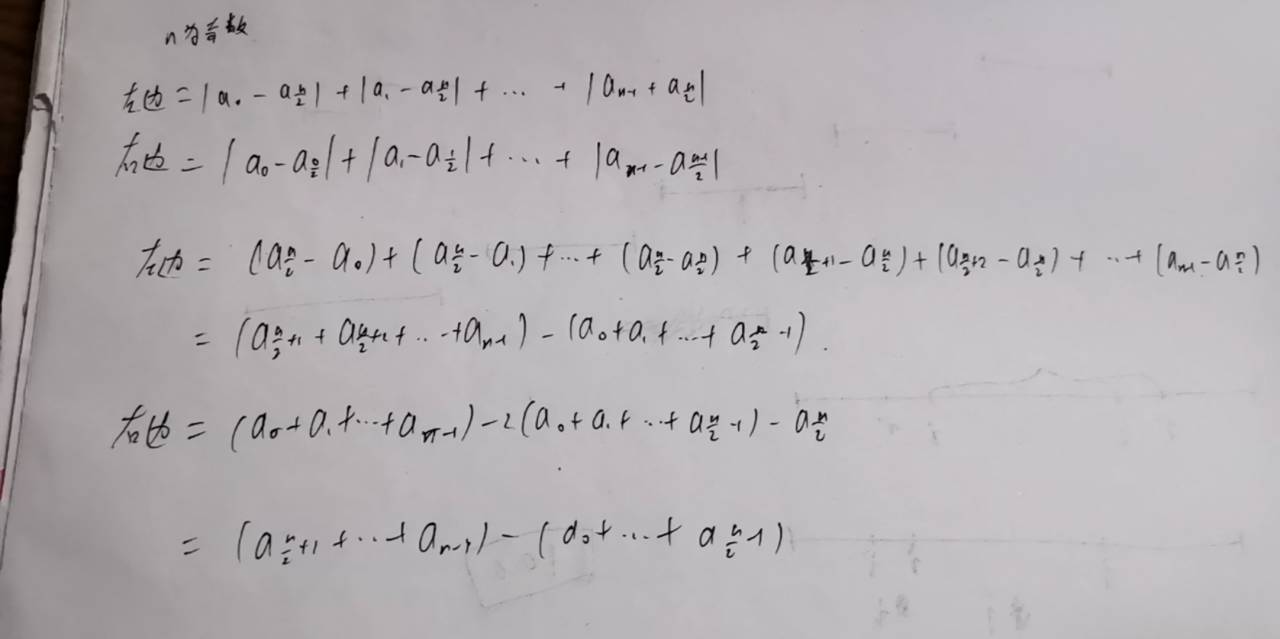
故当 n 为奇数的时候等式两边是相等的
同理可证 n 为偶数的时候等式两边相等
好的这篇题解就水完了


对于任意两个点来说,一个点只要在他们中间的话,那么这个点的位置在哪不影响它到这两个点的距离之和。所以只要保证货仓位置两边有相同的点即可
看到有同学说为何不是平均数。如果这个题目要求的是平方距离Σni=1(xi−ˆx)2最小的话,答案就是平均数了。
因为如果使平方距离最小,就可以转化为最优化问题,令J=Σni=1(xi−ˆx)2,要求最优的ˆx,直接对J求关于ˆx的导数后等于零即可。最后可以解出ˆx=1nΣni=1xi
可是求绝对值最小和求平方差最小差距在哪里呢,不能转换么
比如1 3 3,你看这个数据,如果建在平均数这里,就是2,距离和为3。但如果建在中位数3处,就是2了。
正是因为前者有加个平方,导致平方和的最小值并不是绝对值和的最小值。
ab<=0,((|a|+|b|)^2)^(1/2)=|a|+|b|>=(a^2+2|a||b|+b^2)^(1/2)
是中位数吧
int res = 0; for(int i = 0; i < n / 2; i ++ ) res += (q[n - i - 1] - q[i]);还可以这么写,因为如果是偶数的话,排完序之后最大减最小就是它们之间的距离,如果是奇数的话,最中间的那个数就可以不需要考虑,因为只需要把店子放在那个点就可以啦
stO Orz
orz
orz
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
hh
???
orz
汤老师,怎么这里也能看见你
几何上就是将三角形的面积有以n/2为中界所隔成的两个小三角形面积转化成了以n/2竖线所交斜边后平行的右节点所围成的一个大三角形面积hh
#include<iostream> #include<algorithm> using namespace std; int n; int a[100005]; int main() { cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; } sort(a+1,a+1+n); long long ans=0; for(int l=1,r=n;r>l;l++,r--) { ans+=a[r]-a[l]; } cout<<ans; return 0; }0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
orz
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
6
如果我的商店坐标是1 3 3,那结果不应该是3吗?
结果是2, 奇数个商店的话定位一定在正中间也就是3这个点
Orz
22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222
OrzOrzOrzOrzOrzOrzOrzOrzOrzOrz
orz
orz
# Orz
nice!
算距离res的时候可以依次计算a[]首尾的元素之间的距离,这样只用循环n/2次
for (int i = 0; i < n / 2; i++) res += a[n - i - 1] - a[i];求中位数直接nth_element不是更快吗
nth_element比sort快了35ms
是这么回事。
这么说的话求和用accumulate更快()