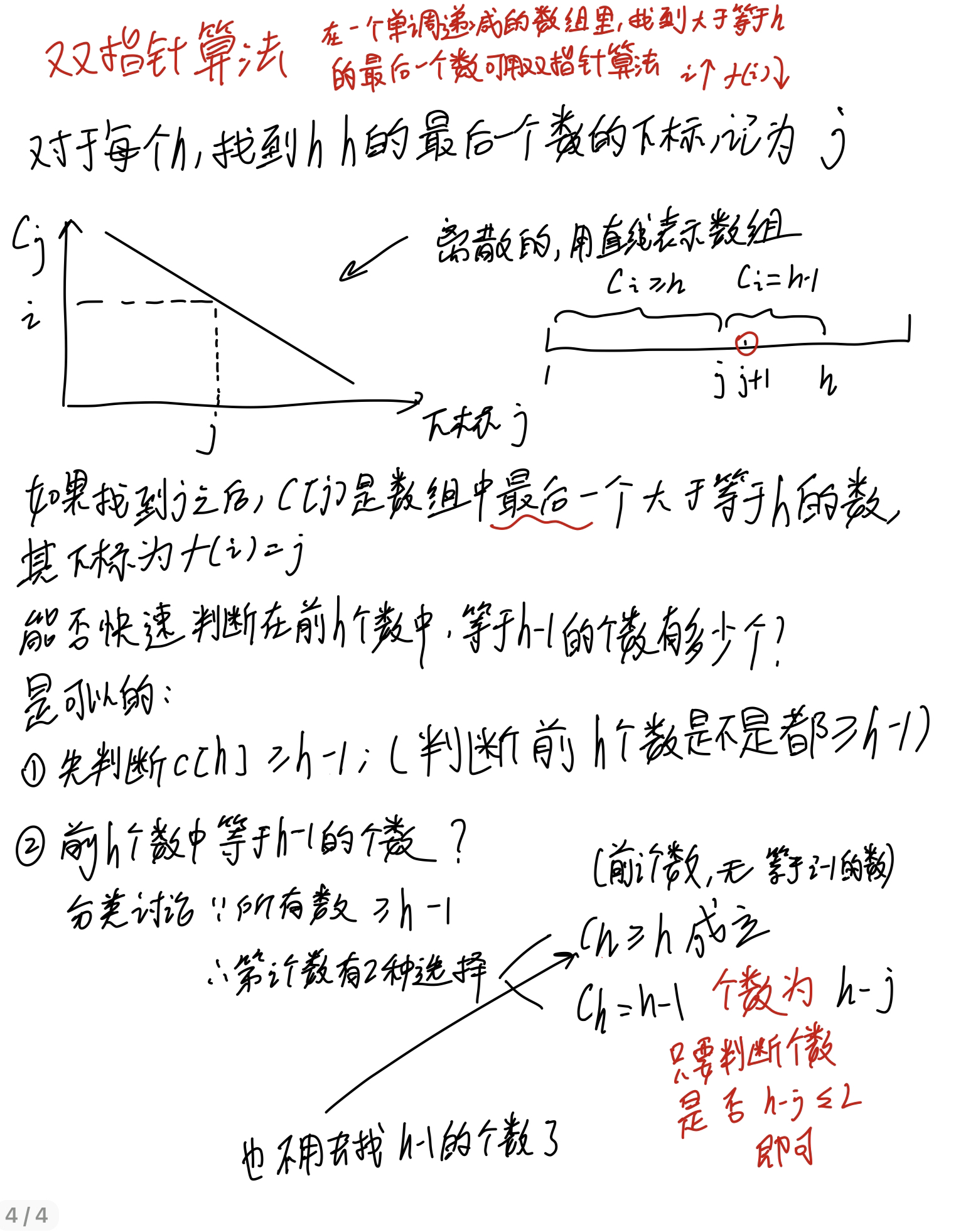
思路&做法

隐含条件：新写的论文的引用次数记为0

如何得到h指数呢？
从大到小排序后，看前h个数是不是都大于等于h？

如果可以选择L个数加1的话，我们又如何判断呢？这就不要求前h个数大于等于h了，有的数可以小于h

那么一般情况是这样的，如下图

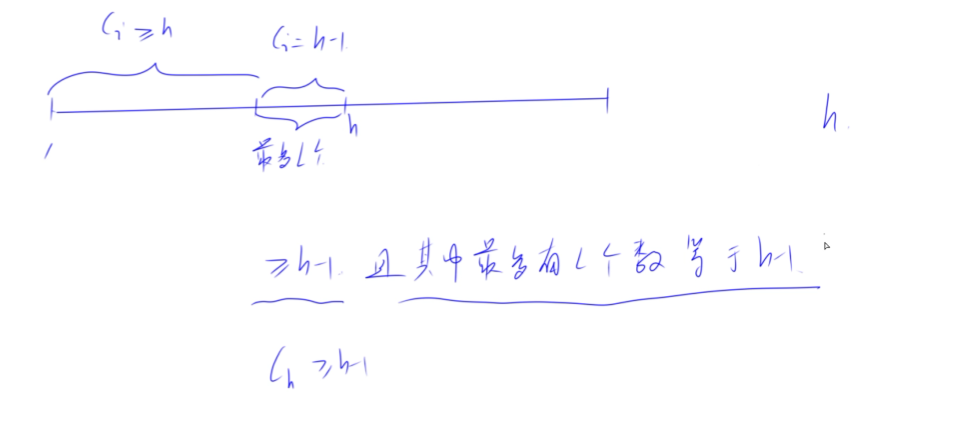
题目要求如下：
（1）在给定的n个数中，从大到小排序后，在前h个数中是不是所有的数都大于等于h - 1，并且其中最多只能有L个数等于h - 1。如果满足上述条件的话，则h成立。

题目要求我们找到满足条件的最大的h的值是多少。

做法

（1）对于判断前h个数是不是所有的数都大于等于h - 1，直接判断c[h]（下标从1开始）是不是大于等于h - 1即可，因为h数组已经从大到小排完序了

（1）可以使用二分，二分出h，然后去暴力判断是不是满足要求$O(logn)$

（2）这里重点记录双指针的做法：

双指针算法可以将除了排序优化到 $O(n)$

使用双指针算法一定要找到单调性，才能使用

对于每一个h，我们要找到前h个数中等于h - 1的数量

Code1 双指针

import java.util.Arrays;
import java.util.Scanner;

public class Main{
    static int N = 100010;
    static int n, L;
    static int [] w = new int [N];
    static int [] temp = new int [N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        L = sc.nextInt();

        for(int i = 1; i <= n; i ++)  temp[i] = sc.nextInt();
        Arrays.sort(temp, 1, n + 1);
        for(int i = 1; i <= n; i ++){
            w[i] = temp[n + 1 - i];
        }

        int res = 0;
        for(int i = 1, j = n; i <= n; i ++){
            //因为我们的j下标表示的是大于等于i的最右边也就是最后一个数
            //那么一旦w[j] >= i 就要停止下来
            //那么相对而言的话，一旦w[j] >= j的话，j就要向左边走
            //j指向的数逐渐变大
            while(j > 0 && w[j] < i) j --;
            if(w[i] >= i - 1 && i - j <= L)
                res = i;
            //这里也不需要让res每次比较取最值，因为i是不断变大的
        }
        System.out.println(res);
    }
}

Code2 二分

import java.util.Scanner;

public class Main{
    //二分入手点就是两个：
    //我们要的答案具有二段性的特点：即一段是成立的，一段是不成立的，我们要求左边界或者右边界
    //容易实现的check函数，这是能不能写出二分的关键！！！

    //二分就是从给定的序列中，最多挑L个数 + 1后，能否找到h个数大于等于h?
    //二分的过程好做
    //二分的难点就是check函数，如何判断，并且想要二分必须具有二段性
    //单调性一定可以二分，但是二分不一定需要单调性
    //这里的h，假设较大的h1如果满足的话，那么hi <= h1 , hi一定是可以满足的

    //我们这里主要去思考如何去编写check函数？
    //一、O(n) 时间统计
    //（1）统计大于等于h的数的个数 （这些数已经满足要求，不需要加1）
    //（2）统计h - 1的个数 （只有加在这些数，才能有可能满足要求，加在<h - 1的数上面也没用）

    //那么最多可以将多少个h - 1的数变成h呢？ t = min{L, b}
    //最后得到的 >= h 的数量就是 count = t + a 
    //判断是不是count >= h 即可

    //----------------- CODE ---------------------
    static int N = 100010;
    static int [] w = new int [N];
    static int n, L;

    static boolean check(int h) {
        int a = 0; //表示大于等于h的数的个数
        int b = 0; //表示大小是h - 1的个数

        for(int i = 1; i <= n; i ++){
            if(w[i] >= h) a ++;
            else {
                if(w[i] == h - 1) b ++;
            }
        }

        return Math.min(b, L) + a >= h ? true : false;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        L = scanner.nextInt();
        for(int i = 1; i <= n; i ++) w[i] = scanner.nextInt();

        //当然答案有可能是0，所以在这里应该l从0开始枚举
        //奶牛贝茜可能一篇论文也没发表，就像我一样
        int l = 0, r = N;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(check(mid)) l = mid;
            else r = mid - 1;
        }

        System.out.println(l);
    }
}